题目内容
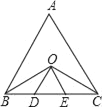
【题目】如图,△ACD中,∠ACD=60°,以AC为边作等腰三角形ABC,AB=AC,E、F分别为边CD、BC上的点,连结AE、AF、EF,∠BAC=∠EAF=60°
(1)求证:△ABF≌△ACE;
(2)若∠AED=70°,求∠EFC的度数;
(3)请直接指出:当F点在BC何处时,AC⊥EF?

【答案】(1)见解析;(2)∠EFC=10°;(3)当F点是BC的中点时,AC⊥EF.理由见解析.
【解析】
(1)由等边三角形性质得到∠B=∠ACB=(180°-6°)÷2=60°,所以∠ACD=∠D,又∠BAC-∠CAF=∠EAF-∠CAF,即∠EAC=∠BAF,又AB=AC,所以得到△CAE≌△BAF. (2)由△CAE≌△BAF,得到AE=AF,∠AEC=∠AFB,有∠AEF=∠AFE=(180°-60°)÷2=60°,又因∠AEC+∠AED=∠AFC+∠AFB=180°,得到∠AED=∠AFC=70°,所以∠EFC=∠AFC-∠AFE=70°-60°=10°. (3)△CAE≌△BAF得到AE=AF,CE=BF,又因BF=CF,所以CE=CF,即得到AC⊥EF
(1)证明:∵∠BAC=∠EAF=60°,
∴∠BAC-∠CAF=∠EAF-∠CAF,
∴∠EAC=∠BAF,
∵AB=AC,
∴∠B=∠ACB=(180°-6°)÷2=60°,
∵∠ACD=60°,
∴∠ACD=∠D,
在△CAE和△BAF中,
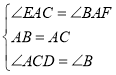 ,
,
∴△CAE≌△BAF.
(2)解:∵△CAE≌△BAF,
∴AE=AF,∠AEC=∠AFB,
∴∠AEF=∠AFE=(180°-60°)÷2=60°,
∵∠AEC+∠AED=∠AFC+∠AFB=180°,
∴∠AED=∠AFC=70°,
∴∠EFC=∠AFC-∠AFE=70°-60°=10°.
(3)解:当F点是BC的中点时,AC⊥EF.
理由:∵△CAE≌△BAF.
∴AE=AF,CE=BF,
∵BF=CF,
∴CE=CF,
∴AC⊥EF.