题目内容
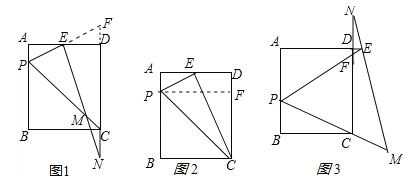
【题目】如图1,矩形ABCD中,P是AB边上的一点(不与A,B重合),PE平分∠APC交射线AD于E,过E作EM⊥PE交直线CP于M,交直线CD于N.
(1)求证:CM=CN;
(2)若AB:BC=4:3,
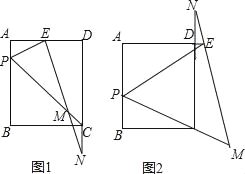
①当![]() = 时,E恰好是AD的中点;
= 时,E恰好是AD的中点;
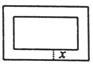
②如图2,当△PEM与△PBC相似时,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】试题分析:(1)由矩形的性质得出∠A=∠ADC=90°,AB=CD,AD=BC,由平行线的性质、互余两角关系、对顶角相等以及角平分线证出∠CMN=∠N,即可得出结论;
(2)①由题意得出M、N、C三点重合,由ASA证明△APE≌△DFE,得出AP=DF,PE=FE,由线段垂直平分线的性质证出AP+CD=PC,设AD=3,AB=4,过P作PF⊥CD于F,设AP=DE=x,则PB=CF=4﹣x,PC=4+x,PF=3,由勾股定理得出方程,解方程即可;
②分两种情况:1.若△PEM∽△CCBP,则∠EPM=∠BCP,得出PE∥BC,不成立;
2.若△PEM∽△PBC,则∠APB=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB=![]() a,AP=(
a,AP=(![]() )a,AE=(
)a,AE=(![]() )a,设PE与CD交于点F,证出△PEM∽△FEN,由相似三角形的性质和平行线分线段成比例定理得出
)a,设PE与CD交于点F,证出△PEM∽△FEN,由相似三角形的性质和平行线分线段成比例定理得出![]() ,即可得出结果.
,即可得出结果.
试题解析:解:(1)延长PE交CD的延长线于F,如图1所示:
∵四边形ABCD是矩形,∴AB∥CD,∠A=∠ADC=∠EDF═90°,AB=CD,AD=BC,∴∠APE+∠AEP=90°,∴∠F=∠APE,∵EM⊥EN,∴∠PEN=∠FEN=90°,∴∠CPE+∠PME=90°,∠F+∠N=90°,∵PE平分∠APC,∴∠APE=∠MPE,又∵∠PME=∠CMN,∴∠CMN=∠N,∴CM=CN;
(2)①若E是AD的中点,则M、N、C三点重合,∵E为AD的中点,∴AE=DE,在△APE和△DFE中,∵∠A=∠EDF,AE=DE,∠AEP=∠DEF,∴△APE≌△DFE(ASA),∴AP=DF,PE=FE,∵EM⊥EN,∴PC=FC,∵FC=CD+DF,∴AP+CD=PC,设AD=3a,AB=4a,过P作PF⊥CD于F,如图2所示:
设AP=DE=x,则PB=CF=4﹣x,PC=4+x,PF=3,由勾股定理得:(4﹣x)2+32=(4+x)2,解得:x=![]() a,4﹣x=
a,4﹣x=![]() a,∴
a,∴![]() =
=![]() ;
;
②分两种情况:
1.若△PEM∽△CCBP,则∠EPM=∠BCP,∴PE∥BC,不成立;
2.若△PEM∽△PBC,则∠APE=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB=![]() a,AP=(
a,AP=(![]() )a,AE=(
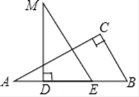
)a,AE=(![]() )a,设PE与CD交于点F,如图3所示:
)a,设PE与CD交于点F,如图3所示:
∵AB∥CD,∴∠EFN=∠BFC=∠APE=60°,∴∠N=∠M=90°﹣60°=30°,∵EM⊥PE,∴∠NEF=∠PEM=90°,∴△PEM∽△FEN,∴ ![]() ,∵AB∥CD,∴
,∵AB∥CD,∴![]() ,∴
,∴![]() =
=![]() =
=![]() .
.