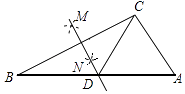
[题目]已知:如图.E.F是四边形ABCD的对角线AC上的两点.AF=CE.DF=BE.DF∥BE．求证:(1)△AFD≌△CEB．(2)四边形ABCD是平行四边形．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．

求证：（1）△AFD≌△CEB．（2）四边形ABCD是平行四边形．

【答案】证明见解析

【解析】证明：（1）∵DF∥BE，

∴∠DFE=∠BEF．

又∵AF=CE，DF=BE，

∴△AFD≌△CEB（SAS）．

（2）由（1）知△AFD≌△CEB，

∴∠DAC=∠BCA，AD=BC，

∴AD∥BC．

∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）．

（1）利用两边和它们的夹角对应相等的两三角形全等（SAS），这一判定定理容易证明△AFD≌△CEB．

（2）由△AFD≌△CEB，容易证明AD=BC且AD∥BC，可根据一组对边平行且相等的四边形是平行四边形．

练习册系列答案

（1）求证：CE∥DF；

（2）若∠DCE＝126°，求∠DEF的度数．

【题目】如图，将三角形ABC向右平移5个单位长度，再向上平移3个单位长度请回答下列问题：

（1）平移后的三个顶点坐标分别为：A1　　，B1　　，C1　　；

（2）画出平移后三角形A1B1C1；

（3）求三角形ABC的面积．

【题目】在平面直角坐标系xOy中，⊙C的半径为r（r＞1），P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：若直线CP与⊙C交于点A，B，满足|PA﹣PB|=2，则称点P为⊙C的“完美点”，如图为⊙C及其“完美点”P的示意图．

（1）当⊙O的半径为2时，
①点M（，0）⊙O的“完美点”，点N（0，1）⊙O的“完美点”，点T（﹣ ，﹣ ）⊙O的“完美点”（填“是”或者“不是”）；
②若⊙O的“完美点”P在直线y= x上，求PO的长及点P的坐标；
（2）⊙C的圆心在直线y= x+1上，半径为2，若y轴上存在⊙C的“完美点”，求圆心C的纵坐标t的取值范围．

【题目】在四边形ABCD中，AC⊥BD，AB＝AD，要使四边形ABCD是菱形，只需添加一个条件，这个条件可以是_____（只要填写一种情况）．

【题目】如图1，在平面直角坐标系xOy中，点A的坐标为（0，1），取一点B（b，0），连接AB，做线段AB的垂直平分线l1 ，过点B作x轴的垂线l2 ，记l1 ， l2的交点为P．

（1）当b=3时，在图1中补全图形（尺规作图，不写作法，保留作图痕迹）；
（2）小慧多次取不同数值b，得出相应的点P，并把这些点用平滑的曲线连接起来发现：这些点P竟然在一条曲线L上！
①设点P的坐标为（x，y），试求y与x之间的关系式，并指出曲线L是哪种曲线；
②设点P到x轴，y轴的距离分别是d1 ， d2 ，求d1+d2的范围，当d1+d2=8时，求点P的坐标；
③将曲线L在直线y=2下方的部分沿直线y=2向上翻折，得到一条“W”形状的新曲线，若直线y=kx+3与这条“W”形状的新曲线有4个交点，直接写出k的取值范围．

【题目】如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC的一半长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连结CD，若AC=5，AB=11，则△ACD的周长为（）

A.11
B.16
C.21
D.27

【题目】在平面直角坐标系中，点A、B、C、D是坐标轴上的点且点C坐标是（0，﹣1），AB=5，点（a，b）在如图所示的阴影部分内部（不包括边界），已知OA=OD=4，则a的取值范围是（）
A.
B.
C.
D.

【题目】如图，ABCD中，AB=13，AD=10，将ABCD沿AE翻折后，点B恰好与点C重合，则点C到AD的距离为（）
A.5
B.12
C.3
D.

试题分类