题目内容
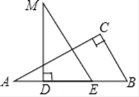
【题目】如图，矩形ABCD中，AB＝12，点E是AD上的一点，AE＝6，BE的垂直平分线交BC的延长线于点F，连接EF交CD于点G．若G是CD的中点，则BC的长是__________．
【答案】10.5
【解析】
利用ASA定理证明△EDG≌△FCG，从而求得DE=CF，EG=GF=
，根据矩形的性质，设BC=x,则DE=x-6，DG=6，BF=2x-6，根据垂直平分线的性质求得EG=
，然后根据勾股定理列方程求解即可．
解：在矩形ABCD中，AD=BC，AB=CD=12，∠D=∠DCF=90°
∵G为CD中点，∴DG=CG
又∵∠EGD=∠FGC
∴△EDG≌△FCG
∴DE=CF，EG=GF=
设BC=x,则DE=AD-AE=BC-AE=x-6，DG=CG=
=6，BF=BC+CF=BC+DE=2x-6，
又∵BE的垂直平分线交BC的延长线于点F，
∴EG=GF=
∴在Rt△EDG中，
解得：x=10.5
则BC的长是10.5
故答案为：10.5．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
