题目内容
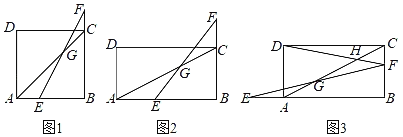
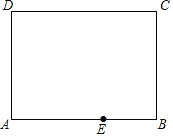
【题目】如图是一张矩形纸片ABCD,已知AB=8,AD=6,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在矩形ABCD的某一条边上,则等腰三角形AEP的底边上的高的长是_____.
【答案】![]() 或
或![]() 或6
或6
【解析】
分情况讨论:①当AP=AE=5时,则△AEP是等腰直角三角形,得出底边PE=![]() AE=5
AE=5![]() ,由等腰直角三角形的性质可求AH的长;
,由等腰直角三角形的性质可求AH的长;
②当P'E=AE=5时,求出BE,由勾股定理求出P'B,再由勾股定理求出AP',由锐角三角函数可求EM的长;
③当P'A=P'E时,由平行线间距离处处相等,可求AD=6,即可得出结论.
解:①当AP=AE=5时,如图所示:过点A作AH⊥PE于H,
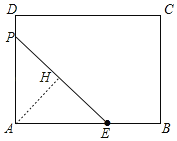
∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=![]() AE=5
AE=5![]() ,
,
∵AH⊥PE,△AEP是等腰直角三角形,
∴AH=![]() PE=
PE=![]() ;
;
②当P'E=AE=5时,
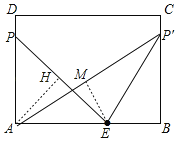
∵BE=AB﹣AE=8﹣5=3,∠B=90°,
∴P'B=![]() =4,
=4,
∴底边AP'=![]() =
=![]() =4
=4![]() ,
,
∵tan∠P'AB=![]() ,
,
∴![]() ,
,
∴ME=![]() ;
;
③当P'A=P'E时,
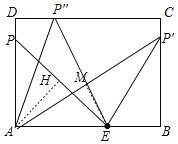
∵AB∥CD,
∴底边AE的高为AD=6;
综上所述:等腰三角形AEP的底边上的高的长是![]() 或
或![]() 或6.
或6.
故答案为:![]() 或
或![]() 或6.
或6.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目