题目内容
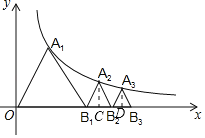
【题目】如图,已知等边△OA1B1,顶点A1在双曲线y=![]() (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.

【答案】(2![]() ,0).
,0).
【解析】根据等边三角形的性质以及反比例函数图象上点的坐标特征分别求出B2、B3、B4的坐标,得出规律,进而求出点B6的坐标.
如图,作A2C⊥x轴于点C,设B1C=a,则A2C=![]() a,
a,
OC=OB1+B1C=2+a,A2(2+a,![]() a).
a).
∵点A2在双曲线y=![]() (x>0)上,
(x>0)上,
∴(2+a)![]() a=
a=![]() ,
,
解得a=![]() ﹣1,或a=﹣
﹣1,或a=﹣![]() ﹣1(舍去),
﹣1(舍去),
∴OB2=OB1+2B1C=2+2![]() ﹣2=2
﹣2=2![]() ,
,
∴点B2的坐标为(2![]() ,0);
,0);
作A3D⊥x轴于点D,设B2D=b,则A3D=![]() b,
b,
OD=OB2+B2D=2![]() +b,A2(2
+b,A2(2![]() +b,
+b,![]() b).
b).
∵点A3在双曲线y=![]() (x>0)上,
(x>0)上,
∴(2![]() +b)
+b)![]() b=
b=![]() ,
,
解得b=﹣![]() +
+![]() ,或b=﹣
,或b=﹣![]() ﹣
﹣![]() (舍去),
(舍去),
∴OB3=OB2span>+2B2D=2![]() ﹣2
﹣2![]() +2
+2![]() =2
=2![]() ,
,
∴点B3的坐标为(2![]() ,0);
,0);
同理可得点B4的坐标为(2![]() ,0)即(4,0);
,0)即(4,0);
…,
∴点Bn的坐标为(2![]() ,0),
,0),
∴点B6的坐标为(2![]() ,0),
,0),
故答案为:(2![]() ,0).
,0).

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目