Question

【题目】如图，楼房BD的前方竖立着旗杆AC．小亮在B处观察旗杆顶端C的仰角为45°，在D处观察旗杆顶端C的俯角为30°，楼高BD为20米．

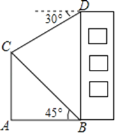
（1）求∠BCD的度数；

（2）求旗杆AC的高度．

Answer 1

【答案】（1）75°；（2）米

【解析】

（1）过点C作CE⊥BD于E，则DF∥CE，AB∥CE，利用平行线的性质求得相关角的度数；

（2）在Rt△ECD、Rt△BCE中，利用正切三角函数解这两个直角三角形，求得CE的长度，进而即可求出答案．

（1）过点C作CE⊥BD于E，则DF∥CE，AB∥CE

∵DF∥CE

∴∠ECD＝∠CDF＝30°，

同理∠ECB＝∠ABC＝45°，

∴∠BCD＝∠ECD+∠ECB＝75°；

（2）在Rt△ECD中，∠ECD＝30°，

∵ ，

∴，

同理：BE＝CE，

∵BD＝BE+DE，

∴，解得：，

∴AC=BE=CE=，

答：旗杆AC的高度为米．