��Ŀ����
����Ŀ��[�Ķ�����]
���조ƽ�а����͡�ȫ��������ģ����֤���߶���ȵ�һ�ַ��������dz������ַ���֤���߶ε��е����⣮
���磺��ͼ��D�ǡ�ABC��AB��һ�㣬E��AC���е㣬����C��CF��AB����DE���ӳ����ڵ�F������֤E���߶�DF���е㣮
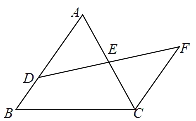
[��������]
�����������Ķ������������۵ľ���ͷ�������������⣮
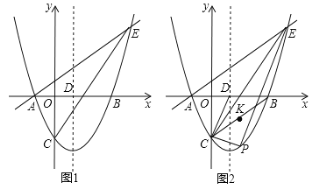
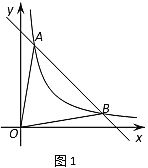
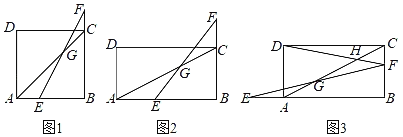
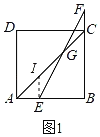
��1����ͼ1����������ABCD�У���E��AB�ϣ���F��BC���ӳ����ϣ�������AE��CF������EF��AC�ڵ�G��
��֤����G��EF���е㣻
��CG��![]() BE��
BE��
[��չ����]
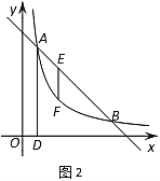
��2����ͼ2���ھ���ABCD�У�AB��2BC����E��AB�ϣ���F��BC���ӳ����ϣ�������AE��2CF������EF��AC�ڵ�G��̽��BE��CG֮���������ϵ����˵�����ɣ�
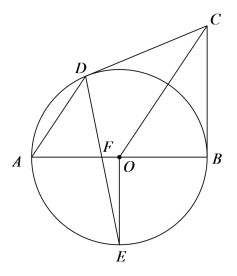
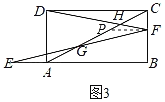
��3����ͼ3������E��BA���ӳ����ϣ���F���߶�BC�ϣ�DF��AC�ڵ�H��BF��2��CF��1���� 2���е������������䣬��ֱ��д��GH�ij���
���𰸡���1��������������������������2��BE��![]() CG�����������������3��
CG�����������������3��![]() ��
��
��������
��1���ٹ���E��EI��BC��AC�ڵ�I��֤����EIG�ա�FCG��ASA�����ó�EG��FG���ɣ�
���ɵ���ֱ�������ε����ʵó� AI��![]() AE����ƽ���ߵó�
AE����ƽ���ߵó�![]() ��
��![]() ��
��![]() ��֤��IC��
��֤��IC��![]() BE����ȫ�������ε����ʵó�IG��CG��
BE����ȫ�������ε����ʵó�IG��CG��![]() IC�����ɵó����ۣ�
IC�����ɵó����ۣ�
��2����EI��BC ��AC�ڵ�I�������Ǻ���֤��AE��2IE���ó�IE��CF��֤��EIG�ա�FCG��ASA�����ó�EG��FG��IG��CG����IE��a����AE��2a�����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ���ó�IC��
���ó�IC��![]() EB�����ɵó������
EB�����ɵó������
��3����FP��AB��AC��P����FP��CD����CFP����ABC��90������CPF����CAB����tan��CPF��![]() ��tan��CAB��
��tan��CAB��![]() ��
��![]() �����AE��PF��2��BC��3��CD��AB��2BC��6��AC��3
�����AE��PF��2��BC��3��CD��AB��2BC��6��AC��3![]() ��֤����CPF�ס�CAB���ó�
��֤����CPF�ס�CAB���ó�![]() ��
��![]() ��
��![]() �����PC��
�����PC��![]() AC��
AC��![]() ��PA��2
��PA��2![]() ��AG��PG��
��AG��PG��![]() ����֤����PFH�ס�CDH���ó�
����֤����PFH�ס�CDH���ó�![]() ��
��![]() ��
��![]() ���ó�PH��
���ó�PH��![]() PC��
PC��![]() �����ɵó������
�����ɵó������
��1��֤����������E��EI��BC��AC�ڵ�I����ͼ1��ʾ��
���ı���ABCD�������Σ�
��AB��BC����AEI����ABC��90�㣬
���BAC��45�㣬
���AIE����BAC��45�㣬
��AE��EI��
��AE��CF��
��CF��EI��
��EI��BC��
���EIG����FCG����IEG����CFG��
�ڡ�EIG�͡�FCG�У�
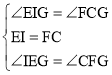 ��
��
���EIG�ա�FCG��ASA����
��EG��FG��
��G��EF���е㣻
����Rt��AEI�У���AEI��90�㣬AE��EI��
���AEI�ǵ���ֱ�������Σ�
��AI��![]() AE��
AE��
��![]() ��
��![]() ��
��
��EI��BC��
��![]() ��
��![]() ��
��![]() ��
��
��IC��![]() BE��
BE��
�ߡ�EIG�ա�FCG��
��IG��CG��![]() IC��
IC��
��CG��![]() ��
��![]() BE��
BE��![]() BE��
BE��
��2���⣺BE��CG֮���������ϵΪ��BE��![]() CG���������£�
CG���������£�
����E��EI��BC ��AC�ڵ�I����ͼ2��ʾ��
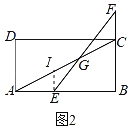
���ı���ABCD�Ǿ��Σ�
���AEI����ABC��90�㣬AB��CD��AB��CD��
��Rt��AEI��Rt��ABC�У���ABC����AEI��90�㣬AB��2BC��
��tan��IAE��![]() ��
��![]() ��
��![]() ��
��
��AE��2IE��
��AE��2CF��
��IE��CF��
��EI��BC��
���EIG����FCG����IEG����CFG��
�ڡ�EIG�͡�FCG�У�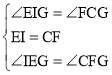 ��
��
���EIG�ա�FCG��ASA����
��EG��FG��IG��CG��
��IE��a����AE��2a��
��Rt��AEI�У���AEI��90�㣬
��AI��![]() ��
��![]() ��
��![]() a��cos��IAE��
a��cos��IAE��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��EI��BC��
��![]() ��
��![]() ��
��![]() ��
��
��IC��![]() EB��
EB��
��IG��CG��![]() IC��
IC��
��CG��![]() BE��
BE��
��BE��![]() CG��
CG��
��3���⣺��FP��AB��AC��P����ͼ3��ʾ��
��FP��CD����CFP����ABC��90�㣬��CPF����CAB��
��Rt��CFP��Rt��ABC��AB��2BC��
��tan��CPF��![]() ��tan��CAB��
��tan��CAB��![]() ��
��![]() ��
��
��PF��2CF��
��AE��2CF��
��AE��PF��2��
ͬ��2���ã���AEG�ա�PFG��AAS����
��AG��PG��
��BF��2��CF��1��
��BC��3��CD��AB��2BC��6��
��AC��![]() ��
��![]() ��3
��3![]() ��
��
��FP��AB��
���CPF�ס�CAB��
��![]() ��
��![]() ��
��![]() ��
��
��PC��![]() AC��
AC��![]() ��PA��AC��PC��2
��PA��AC��PC��2![]() ��
��
��AG��PG��![]() PA��
PA��![]() ��
��
��FP��CD��
���PFH�ס�CDH��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��PH��![]() PC��
PC��![]() ��
��
��GH��PG+PH��![]() ��
��![]() ��
��

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�