题目内容
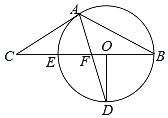
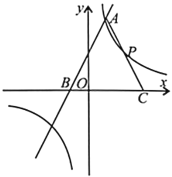
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D为的![]() 中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
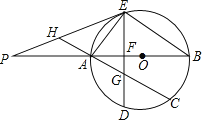
(1)求证:PE是⊙O的切线;
(2)连接CA与DE相交于点G,CA的延长线交PE于H,求证:HE=HG;
(3)若tan∠P=![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OE,由圆周角定理证得∠EAB+∠B=90°,可得出∠OAE=∠AEO,则∠PEA+∠AEO=90°,即∠PEO=90°,则结论得证;
(2)连接OD,证得∠AOD=∠AGF,∠B=∠AEF,可得出∠PEF=2∠B,∠AOD=2∠B,可证得∠PEF=∠AOD=∠AGF,则结论得证;
(3)可得出tan∠P=tan∠ODF=![]() ,设OF=5x,则DF=12x,求出AE,BE,得出
,设OF=5x,则DF=12x,求出AE,BE,得出![]() ,证明△PEA∽△PBE,得出
,证明△PEA∽△PBE,得出![]() ,过点H作HK⊥PA于点K,证明∠P=∠PAH,得出PH=AH,设HK=5a,PK=12a,得出PH=13a,可得出AH=13a,AG=10a,则可得出答案.
,过点H作HK⊥PA于点K,证明∠P=∠PAH,得出PH=AH,设HK=5a,PK=12a,得出PH=13a,可得出AH=13a,AG=10a,则可得出答案.
解:(1)证明:如图1,连接OE,
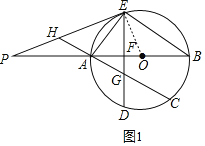
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠B=90°,
∵OA=OE,
∴∠OAE=∠AEO,
∴∠B+∠AEO=90°,
∵∠PEA=∠B,
∴∠PEA+∠AEO=90°,
∴∠PEO=90°,
又∵OE为半径,
∴PE是⊙O的切线;
(2)如图2,连接OD,
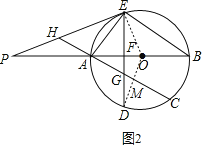
∵D为![]() 的中点,
的中点,
∴OD⊥AC,设垂足为M,
∴∠AMO=90°,
∵DE⊥AB,
∴∠AFD=90°,
∴∠AOD+∠OAM=∠OAM+∠AGF=90°,
∴∠AOD=∠AGF,
∵∠AEB=∠EFB=90°,
∴∠B=∠AEF,
∵∠PEA=∠B,
∴∠PEF=2∠B,
∵DE⊥AB,
∴![]() ,
,
∴∠AOD=2∠B,
∴∠PEF=∠AOD=∠AGF,
∴HE=HG;
(3)解:如图3,
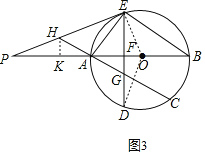
∵∠PEF=∠AOD,∠PFE=∠DFO,
∴∠P=∠ODF,
∴tan∠P=tan∠ODF=![]() ,
,
设OF=5x,则DF=12x,
∴OD=![]() =13x,
=13x,
∴BF=OF+OB=5x+13x=18x,AF=OA﹣OF=13x﹣5x=8x,
∵DE⊥OA,
∴EF=DF=12x,
∴AE=![]() =4
=4![]() x,BE=
x,BE=![]() =6
=6![]() x,
x,
∵∠PEA=∠B,∠EPA=∠BPE,
∴△PEA∽△PBE,
∴![]() ,
,
∵∠P+∠PEF=∠FAG+∠AGF=90°,
∴∠HEG=∠HGE,
∴∠P=∠FAG,
又∵∠FAG=∠PAH,
∴∠P=∠PAH,
∴PH=AH,
过点H作HK⊥PA于点K,
∴PK=AK,
∴![]() ,
,
∵tan∠P=![]() ,
,
设HK=5a,PK=12a,
∴PH=13a,
∴AH=13a,PE=36a,
∴HE=HG=36a﹣13a=23a,
∴AG=GH﹣AH=23a﹣13a=10a,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案