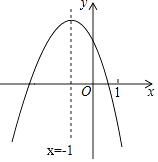ΧβΡΩΡΎ»ί
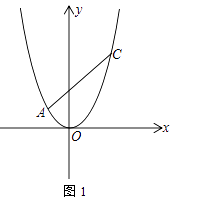
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏy=©¹ ![]() x2+bx+c”κx÷αΫΜ”ΎΒψAΘ®©¹4Θ§0Θ©ΓΔBΘ®6Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ°
x2+bx+c”κx÷αΫΜ”ΎΒψAΘ®©¹4Θ§0Θ©ΓΔBΘ®6Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ°
Θ®1Θ©»γΆΦlΘ§«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ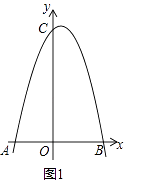
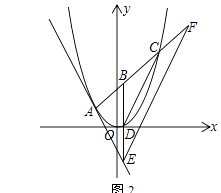
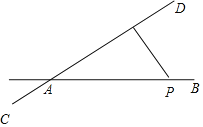
Θ®2Θ©»γΆΦ2Θ§ΒψPΈΣΒΎ“Μœσœό≈ΉΈοœΏ…œ“ΜΒψΘ§Ν§Ϋ”PCΓΔPAΘ§PAΫΜy÷α”ΎΒψFΘ§…ηΒψPΒΡΚαΉχ±ξΈΣtΘ§ΓςCPFΒΡΟφΜΐΈΣSΘ°«σS”κtΒΡΚ· ΐΙΊœΒ ΫΘ®≤Μ“Σ«σ–¥≥ωΉ‘±δΝΩtΒΡ»Γ÷ΒΖΕΈßΘ©ΘΜ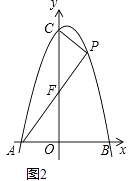
Θ®3Θ©»γΆΦ3Θ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Ν§Ϋ”BCΘ§ΙΐΒψPΉςPDΓΈy÷α±δBC”ΎΒψDΘ§ΒψHΈΣAF÷–ΒψΘ§«“ΒψNΘ®0Θ§1Θ©Θ§Ν§Ϋ”NHΓΔBHΘ§ΫΪΓœNHB»ΤΒψHΡφ ±’κ–ΐΉΣΘ§ ΙΫ«ΒΡ“ΜΧθ±ΏH¬δ‘Ύ…δœΏHF…œΘ§Νμ“ΜΧθ±ΏHN±δ≈ΉΈοœΏ”ΎΒψQΘ§Β±BH=BD ±Θ§«σΒψQΉχ±ξΘ°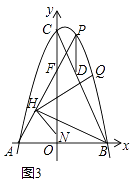
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΫβΘΚΓΏ≈ΉΈοœΏy=©¹ ![]() x2+bx+cΙΐΒψAΘ®©¹4Θ§0Θ©Θ§BΘ®6Θ§0Θ©Θ§
x2+bx+cΙΐΒψAΘ®©¹4Θ§0Θ©Θ§BΘ®6Θ§0Θ©Θ§
Γύ 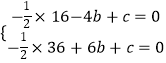 Θ§ΫβΒΟ
Θ§ΫβΒΟ ![]() Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣy=©¹ ![]() x2+x+12Θ°
x2+x+12Θ°
Θ®2Θ©
ΫβΘΚ»γΆΦ1Υυ ΨΘΚΙΐΒψPΉςPRΓΆy÷αΘ§ΫΜy÷α”ΎΒψRΘ§ΙΐΒψPΉςPLΓΆAB”ΎΒψLΘ°
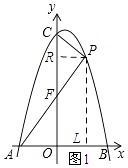
ΒψPΘ®tΘ§©¹ ![]() t2+t+12Θ©Θ§‘ρAL=t+4Θ§PL=©¹
t2+t+12Θ©Θ§‘ρAL=t+4Θ§PL=©¹ ![]() t2+t+12=©¹
t2+t+12=©¹ ![]() Θ®t+4Θ©Θ®t©¹6Θ©Θ°
Θ®t+4Θ©Θ®t©¹6Θ©Θ°
ΓύtanΓœPAL= ![]() =3©¹
=3©¹ ![]() tΘ°
tΘ°
‘ΎRtΓςFAO÷–Θ§tanΓœFAO= ![]() =
= ![]() =3©¹
=3©¹ ![]() tΘ°
tΘ°
ΓύOF=12©¹2tΘ°
ΓύCF=CO©¹OF=12©¹Θ®12©¹2tΘ©=2tΘ§
ΓύSΓςCPF= ![]() CFPR=
CFPR= ![]() ΓΝ2tt=t2Θ°
ΓΝ2tt=t2Θ°
Θ®3Θ©
ΫβΘΚ―”≥ΛPDΫΜx÷α”ΎΒψLΘ§»ΓOAΒΡ÷–ΒψKΘ§Ν§Ϋ”HKΘ§ΙΐΒψHΉςHGΓΆy÷α”ΎΒψGΘ§ΙΐΒψQΉςQMΓΆHG”ΎΒψMΘ°
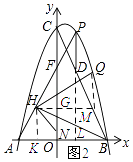
ΓΏOF=12©¹2tΘ§ΒψHΈΣAFΒΡ÷–ΒψΘ§HKΓΆOAΘ§
ΓύHK= ![]() OF=6©¹t=BLΘ°
OF=6©¹t=BLΘ°
ΓΏ‘ΎRtΓςBHKΚΆRtΓςDBL÷–Θ§HK=BLΘ§BH=BDΘ§
ΓύRtΓςBHKΓ’RtΓςDBL
ΓύBK=DL=8Θ°
÷±œΏBCΒΡΫβΈω ΫΈΣy=©¹2x+12Θ§
ΓύΒψDΘ®tΘ§©¹2t+12Θ©Θ°
ΓΏDL=12©¹2t=8Θ§
Γύt=2Θ°
ΓύΒψPΘ®2Θ§12Θ©Θ§ΒψHΘ®©¹2Θ§4Θ©Θ°
ΓύtanΓœAHK=tanΓœHBK= ![]() Θ§
Θ§
ΓύΓœAHK=ΓœHBKΘ§
ΓύΓœAHB=90ΓψΘ°
ΓΏΓœNHB=ΓœPHQΘ§
ΓύΓœNHQ=90ΓψΘ§
ΓύΓœHNG=ΓœQHMΘ°
ΓΏΒψNΘ®0Θ§1Θ©Θ§HG=2Θ§
ΓύGN=3Θ§tanΓœHNG=tanΓœQHM= ![]() Θ§
Θ§ ![]() =
= ![]() Θ°
Θ°
…ηΒψQΘ®mΘ§©¹ ![]() m2+m+12Θ©Θ§QM=©¹
m2+m+12Θ©Θ§QM=©¹ ![]() m2+m+12©¹4=©¹
m2+m+12©¹4=©¹ ![]() m2+m+8Θ§HM=m+2Θ°
m2+m+8Θ§HM=m+2Θ°
Γύ ![]() =
= ![]() Θ§ΫβΒΟΘΚm1=©¹
Θ§ΫβΒΟΘΚm1=©¹ ![]() Θ®…α»ΞΘ©Θ§m2=4Θ§
Θ®…α»ΞΘ©Θ§m2=4Θ§
ΓύΒψQΘ®4Θ§8Θ©Θ°
ΓΨΫβΈωΓΩΘ®1Θ©ΫΪΒψAΓΔBΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏy=©¹ ![]() x2+bx+cΒΡΫβΈω ΫΘ§ΒΟΒΫΙΊ”ΎbΓΔcΒΡΖΫ≥ΧΉιΘ§»ΜΚσΫβΒΟbΓΔcΒΡ÷ΒΦ¥Ω…ΘΜΘ®2Θ©ΙΐΒψPΉςPRΓΆy÷αΘ§ΫΜy÷α”ΎΒψRΘ§ΙΐΒψPΉςPLΓΆAB”ΎΒψLΘ°…ηΒψPΘ®tΘ§©¹
x2+bx+cΒΡΫβΈω ΫΘ§ΒΟΒΫΙΊ”ΎbΓΔcΒΡΖΫ≥ΧΉιΘ§»ΜΚσΫβΒΟbΓΔcΒΡ÷ΒΦ¥Ω…ΘΜΘ®2Θ©ΙΐΒψPΉςPRΓΆy÷αΘ§ΫΜy÷α”ΎΒψRΘ§ΙΐΒψPΉςPLΓΆAB”ΎΒψLΘ°…ηΒψPΘ®tΘ§©¹ ![]() t2+t+12Θ©Θ§‘ρAL=t+4Θ§PL=©¹
t2+t+12Θ©Θ§‘ρAL=t+4Θ§PL=©¹ ![]() Θ®t+4Θ©Θ®t©¹6Θ©Θ§Ω…«σΒΟtanΓœPAL=3©¹
Θ®t+4Θ©Θ®t©¹6Θ©Θ§Ω…«σΒΟtanΓœPAL=3©¹ ![]() tΘ§¥”ΕχΒΟΒΫ=12©¹2tΘ§ΉνΚσ“άΨίSΓςCPF=
tΘ§¥”ΕχΒΟΒΫ=12©¹2tΘ§ΉνΚσ“άΨίSΓςCPF= ![]() CFPR«σΫβΦ¥Ω…ΘΜΘ®3Θ©―”≥ΛPDΫΜx÷α”ΎΒψLΘ§»ΓOAΒΡ÷–ΒψKΘ§Ν§Ϋ”HKΘ§ΙΐΒψHΉςHGΓΆy÷α”ΎΒψGΘ§ΙΐΒψQΉςQMΓΆHG”ΎΒψMΘ° Ήœ»÷ΛΟςRtΓςBHKΓ’RtΓςDBLΘ§¥”ΕχΒΟΒΫBK=DL=8Θ§»ΜΚσ«σΒΟ÷±œΏBCΒΡΫβΈω ΫΘ§…ηΒψDΘ®tΘ§©¹2t+12Θ©Θ§»ΜΚσ”…DL=8Ω…«σΒΟtΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΒψPΚΆΒψHΒΡΉχ±ξΘ§»ΜΚσ‘Ό«σΒΟ
CFPR«σΫβΦ¥Ω…ΘΜΘ®3Θ©―”≥ΛPDΫΜx÷α”ΎΒψLΘ§»ΓOAΒΡ÷–ΒψKΘ§Ν§Ϋ”HKΘ§ΙΐΒψHΉςHGΓΆy÷α”ΎΒψGΘ§ΙΐΒψQΉςQMΓΆHG”ΎΒψMΘ° Ήœ»÷ΛΟςRtΓςBHKΓ’RtΓςDBLΘ§¥”ΕχΒΟΒΫBK=DL=8Θ§»ΜΚσ«σΒΟ÷±œΏBCΒΡΫβΈω ΫΘ§…ηΒψDΘ®tΘ§©¹2t+12Θ©Θ§»ΜΚσ”…DL=8Ω…«σΒΟtΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΒψPΚΆΒψHΒΡΉχ±ξΘ§»ΜΚσ‘Ό«σΒΟ ![]() =
= ![]() Θ§…ηΒψQΘ®mΘ§©¹
Θ§…ηΒψQΘ®mΘ§©¹ ![]() m2+m+12Θ©Θ§‘ρQM=©¹
m2+m+12Θ©Θ§‘ρQM=©¹ ![]() m2+m+8Θ§HM=m+2Θ§ΉνΚσ‘Ό“άΨί
m2+m+8Θ§HM=m+2Θ§ΉνΚσ‘Ό“άΨί ![]() =
= ![]() Ν–ΖΫ≥Χ«σΫβΦ¥Ω…Θ°
Ν–ΖΫ≥Χ«σΫβΦ¥Ω…Θ°

 ’ψΫ≠÷°–«―ß“ΒΥ°ΤΫ≤β ‘œΒΝ–¥πΑΗ
’ψΫ≠÷°–«―ß“ΒΥ°ΤΫ≤β ‘œΒΝ–¥πΑΗ ΗΏ–ß÷«ΡήΩΈ ±Ής“ΒœΒΝ–¥πΑΗ
ΗΏ–ß÷«ΡήΩΈ ±Ής“ΒœΒΝ–¥πΑΗ