题目内容
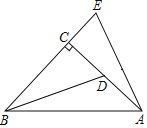
【题目】在△ABC中,∠C=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至G,使CG=BF,连接CE、DE、DG.
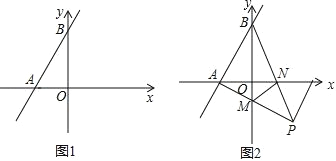
(1)如图1,求证:四边形CEDG是平行四边形 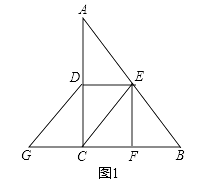 ;
;
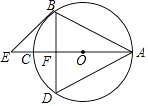
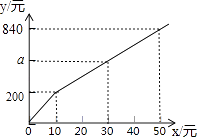
(2)如图2,连接EG交AC于点H,若EG⊥AB,请直接写出图2中所有长度等于 ![]() GH的线段.
GH的线段. 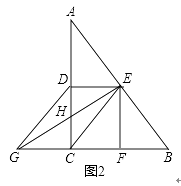
【答案】
(1)证明:如图1中,
∵∠ACB=90°,AE=EB,
∴EC=EA=EB,
∵EF⊥BC,
∴CF=FB,
∵AD=DC,AE=EB,
∴DE∥BC,DE= ![]() BC=BF,
BC=BF,
∵CG=BF,
∴DE=CG,DE∥CG,
∴四边形四边形CEDG是平行四边形
(2)解:如图2中,
∵四边形四边形CEDG是平行四边形,
∴DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,
∵∠A=∠A,∠AEH=∠ADE=90°,
∴△ADE∽△AEH,
∴AE2=ADAH=2a3a=6a2,
∴AE= ![]() a,
a,
在Rt△AEH中,HE= ![]() =
= ![]() =
= ![]() a,
a,
∴AE= ![]() HE,
HE,
∵GH=HE,AE=EB=CE=CD,
∴线段AE、EB、EC、GD都是线段GH的 ![]() 倍
倍
【解析】(1)欲证明四边形CEDG是平行四边形,只要证明DE∥CG,DE=CG即可.(2)由四边形四边形CEDG是平行四边形,推出DH=CH,GH=HE,设DH=CH=a,则AD=CD=2a,由∠A=∠A,∠AEH=∠ADE=90°,推出△ADE∽△AEH,推出AE2=ADAH=2a3a=6a2 , 推出AE= ![]() a,在Rt△AEH中,HE=
a,在Rt△AEH中,HE= ![]() =
= ![]() =
= ![]() a,推出AE=
a,推出AE= ![]() HE,因为GH=HE,AE=EB=CE=CD,即可推出线段AE、EB、EC、GD都是线段GH的
HE,因为GH=HE,AE=EB=CE=CD,即可推出线段AE、EB、EC、GD都是线段GH的 ![]() 倍.
倍.
【考点精析】关于本题考查的三角形中位线定理和平行四边形的判定与性质,需要了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能得出正确答案.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案