题目内容
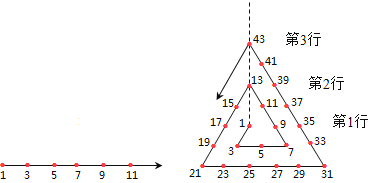
【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上第一行的数是1,第二行的数是13,第三行的数是43,…,依此规律,第五行的数是( )
A. 183 B. 157 C. 133 D. 91
【答案】B
【解析】
观察根据排列的规律得到:所有的数字都是奇数,发生弯折的数与上一个弯折的数的差依次是2,4,6,8…,每一行的数比上次增加连续的三个偶数.依次计算即可得到结论.
所有的数字都是奇数,发生弯折的数与上一个弯折的数的差依次是2,4,6,8…,每一行的数每次增加连续的三个偶数.
第一行数字为1
第二行数字为1+(2+4+6)=1+2(1+2+3)=1+3×4=13
第三行数字为1+(2+4+6)+(8+10+12)=1+2(1+2+3+4+5+6)=1+6×7=43
第四行数字为1+(2+4+6)+(8+10+12)+(14+16+18)=1+2(1+2+3+4+5+6+7+8+9)= 1+9×10=91
第五行数字为1+(2+4+6)+(8+10+12)+(14+16+18)+(20+22+24)
=1+2(1+2+3+4+5+6+7+8+9+10+11+12)=1+12×13=157.
故选B.

练习册系列答案
相关题目