题目内容
【题目】在平面直角坐标系中,抛物线y= ![]() x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
(1)求A、C两点的坐标;
(2)求直线l的解析式;
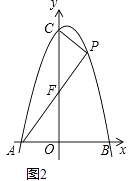
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.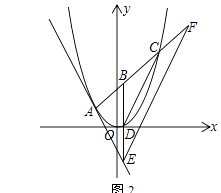
【答案】
(1)
解:∵x1、x2是方程x2﹣2x﹣8的两根,且x1<x2,
∴x1=﹣2,x2=4,
∴A(﹣2,2),C(4,8);
(2)
解:设直线l的解析式为y=kx+b,
∵A(﹣2,2)在直线l上,
∴2=﹣2k+b,
∴b=2k+2,
∴直线l的解析式为y=kx+2k+2①,
∵抛物线y= ![]() x2②,
x2②,
联立①②化简得,x2﹣2kx﹣4k﹣4=0,
∵直线l与抛物线只有一个公共点,
∴△=(2k)2﹣4(﹣4k﹣4)=4k2+16k+16=4(k2+4k+4)=4(k+2)2=0,
∴k=﹣2,
∴b=2k+2=﹣2,
∴直线l的解析式为y=﹣2x﹣2;
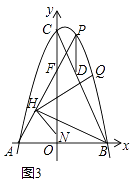
(3)
解:由(1)知,A(﹣2,2),C(4,8),
∴直线AC的解析式为y=x+4,
设点B(m,m+4),
∵(4.8),
∴BC= ![]() |m﹣4|=
|m﹣4|= ![]() (4﹣m)
(4﹣m)
∵过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,
∴D(m, ![]() m2),E(m,﹣2m﹣2),
m2),E(m,﹣2m﹣2),
∴BD=m+4﹣ ![]() m2,BE=m+4﹣(﹣2m﹣2)=3m+6,
m2,BE=m+4﹣(﹣2m﹣2)=3m+6,
∵DC∥EF,
∴△BDC∽△BEF,
∴ ![]() ,
,
∴ ![]() ,
,
∴BF=6 ![]() .
.
【解析】(1)解一元二次方程即可得出点A,C坐标;(2)先设出直线l的解析式,再联立抛物线解析式,用△=0,求出k的值,即可得出直线l的解析式;(3)设出点B的坐标,进而求出BC,再表示出点D,E的坐标,进而得出BD,BE,再判断出△BDC∽△BEF得出比例式建立方程即可求出BF.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案