题目内容
【题目】如图，2条直线相交有1个交点，3条直线相交最多有3个交点，4条直线相交最多有6个交点…按这样的规律若n条直线相交交点最多有28个，则此时n的值为（ ）
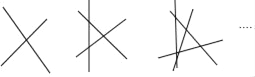
A. 18 B. 10 C. 8 D. 7
【答案】C
【解析】
由2条直线相交时最多有1个交点、3条直线相交时最多有1+2＝3个交点、4条直线相交时最多有1+2+3＝6个交点，…；可知n条直线相交，交点最多有1+2+3+…+n﹣1＝
，再将28代入计算即可．
解：∵2条直线相交时，最多有1个交点；
3条直线相交时，最多有1+2＝3个交点；
4条直线相交时，最多有1+2+3＝6个交点；
…
n条直线相交，交点最多有1+2+3+…+n﹣1＝，
当＝28时，解得：n＝8或﹣7（舍）
故若有8条直线相交，最多有28个交点；
故选：C．
练习册系列答案
相关题目
