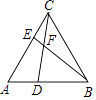题目内容
【题目】已知:如图,在平行四边形ABDC中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.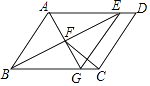
(1)求证:四边形AEGE是菱形;
(2)若∠ABC=60°,AB=4,AD=5,求CF的长.
【答案】
(1)
证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形
∴AD∥BC且AD=BC,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB=∠CBE,∴AB=AE,
∵AF⊥BE,
∴∠AFB=∠GFB=90°,
在△ABF和△GBF中,  ,
,
∴△ABF≌△GBF(ASA),
∴AB=GB,
∴AE=GB,
又∵AD∥BC,
∴四边形ABGE是平行四边形,
又∵AB=GB,
∴四边形ABGE是菱形;
(2)
解:过点F作FM⊥BC于点M,如图所示:
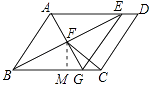
∵四边形ABGE是菱形,
∴∠GBE= ![]() ∠ABC=30°,BG=AB=4,BC=AD=5,
∠ABC=30°,BG=AB=4,BC=AD=5,
在Rt△BFG中,BF=cos∠GBF×BG=cos30°×4= ![]() ×4=2
×4=2 ![]() ,
,
在Rt△BFM中,FM= ![]() BF=
BF= ![]() ×2
×2 ![]() =
= ![]() ,
,
BM=cos∠GBF×BF=cos30°×BF= ![]() ×2
×2 ![]() =3,
=3,
∴CM=BC﹣BM=5﹣3=2,
∴Rt△FMC中,CF= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)先证明AB=AE,由ASA证明△ABF≌△GBF,得出AB=GB,因此AE=GB,证出四边形ABGE是平行四边形,即可得出结论;(2)过点F作FM⊥BC于点M,由菱形的性质得出∠GBE= ![]() ∠ABC=30°,BG=AB=4,BC=AD=5,在Rt△BFG中,由三角函数求出BF=2
∠ABC=30°,BG=AB=4,BC=AD=5,在Rt△BFG中,由三角函数求出BF=2 ![]() ,在Rt△BFM中,求出FM=
,在Rt△BFM中,求出FM= ![]() ,再求出BM=3,得出CM=BC﹣BM=5﹣3=2,Rt△FMC中,由勾股定理即可得出CF的长.
,再求出BM=3,得出CM=BC﹣BM=5﹣3=2,Rt△FMC中,由勾股定理即可得出CF的长.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案