��Ŀ����
����Ŀ����ͼ��һ����·��ʾ��ͼ��![]() �κ�
�κ�![]() �ζ��Ǹ��ţ�
�ζ��Ǹ��ţ�![]() ������������֪
������������֪![]() ��
��![]() ��
��![]() ����
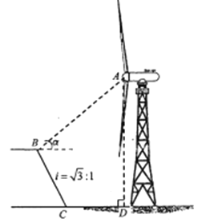
����![]() �θ�������һյ���ƣ�����ʻ��ʱ���ƹ�ɴ�ֱ���䵽�����ϣ���֪����
�θ�������һյ���ƣ�����ʻ��ʱ���ƹ�ɴ�ֱ���䵽�����ϣ���֪����![]() ����������ʻ������������ʱ���ƹ����䵽���ϵ�ʱ����
����������ʻ������������ʱ���ƹ����䵽���ϵ�ʱ����![]() ����ͨ��������ʱ����
����ͨ��������ʱ����![]() ������ӳ�β������
������ӳ�β������![]() ʱ��ʼ��ʱ������ʻ��ʱ��Ϊ
ʱ��ʼ��ʱ������ʻ��ʱ��Ϊ![]() ����ͷ���
����ͷ���![]() �ľ�����
�ľ�����![]() ��
��

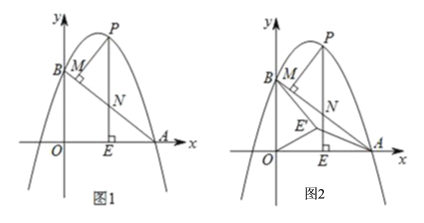
��1�����ٶȺͻij���
��2����![]() ����
����![]() �ĺ�������ʽ��д��
�ĺ�������ʽ��д��![]() ��ȡֵ��Χ��������
��ȡֵ��Χ��������![]() Ϊ��ֵʱ����ͷ��
Ϊ��ֵʱ����ͷ��![]() ����
����![]() �㣮
�㣮
��3����������ȵĻ�������ͬ���ٶ���![]() ������ʻ���һ��Ҳ��������ڻᳵ���ᳵʱ���������������ڣ������Ƚ����������ij�ͷ����
������ʻ���һ��Ҳ��������ڻᳵ���ᳵʱ���������������ڣ������Ƚ����������ij�ͷ����![]() ��ʱ�����ҵij�ͷ�ܷ�
��ʱ�����ҵij�ͷ�ܷ�![]() �㣿���ܵ������ʻ���ص���٣������ܵ�����پ���
�㣿���ܵ������ʻ���ص���٣������ܵ�����پ���![]() �����
�����![]() ��
��
���𰸡���1�����ٶ���![]() ���ij���
���ij���![]() ����2��
����2��![]() ��
��![]() ����3�����ҳ�ͷ���ܵ���
����3�����ҳ�ͷ���ܵ���![]() �㣬���پ���
�㣬���پ���![]() ��
��![]()
��������
��1������ٶ���![]() ���ij���
���ij���![]() ���������г������飬�ⷽ���鼴�ɣ�
���������г������飬�ⷽ���鼴�ɣ�
��2�������⣬�ɷ�Ϊ������ͷ����![]() ��ǰ������ͷ��
��ǰ������ͷ��![]() ��ʱ������ͷ����
��ʱ������ͷ����![]() ��ֱ��������ʽ�����ɵõ��𰸣�
��ֱ��������ʽ�����ɵõ��𰸣�
��3���������⣬�ҳ�������ϵ���г���ʽ���н��⼴�ɣ�
�⣺��1������ٶ���![]() ���ij���
���ij���![]()
�������![]()
���![]()
�𣺻��ٶ���![]() ���ij���
���ij���![]()
��2������ͷ����![]() ��ǰ����
��ǰ����![]() ʱ��
ʱ��
![]()
����ͷ��![]() ��ʱ��
��ʱ��![]() ��
��
����ͷ����![]() ���
���![]() ʱ
ʱ
![]()
����![]()
����ͷ��![]() ��δ����
��δ����![]() ��ʱ��
��ʱ��![]() ��
��
��![]()
���![]()
�൱![]() ʱ����ͷ��
ʱ����ͷ��![]() ��δ����
��δ����![]() �㣻
�㣻
��3���״ӳ�ͷ����![]() �㣬����β�뿪����������ʱ
�㣬����β�뿪����������ʱ![]() ��
��
���Ҫʹ���л��������ڻᳵ���׳�ͷ����![]() ��ʱ�����ҵij�ͷ��
��ʱ�����ҵij�ͷ��![]() ������Ҫ��
������Ҫ��![]() �ij��̣�Ҳ����
�ij��̣�Ҳ����![]() ��
��
��![]()
�൱�׳�ͷ����![]() ��ʱ�����ҳ�ͷ���ܵ���
��ʱ�����ҳ�ͷ���ܵ���![]() �㣬���پ���
�㣬���پ���![]() ��
��![]() ��
��

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�