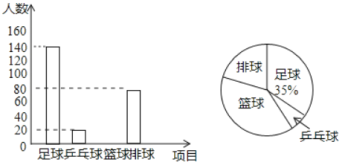
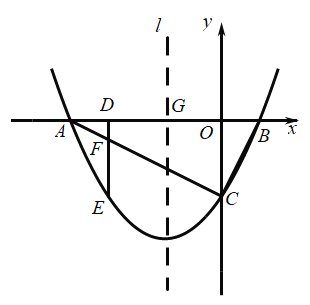��Ŀ����
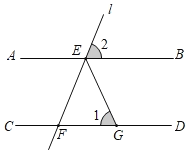
����Ŀ����ͼ������![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ��
��![]() ���ٶ����
���ٶ����![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ��
��![]() ֧���
֧���![]() �˶���������һ������ֹͣʱ��һ������Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊ
�˶���������һ������ֹͣʱ��һ������Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊ![]() ����λ��
�����![]() ����
����![]() �����Ե�
�����Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶�ġ�M������
��Ϊ�뾶�ġ�M������![]() ���߶�
���߶�![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ������
������![]() ��
��
��1����![]() �ij����ú���
�ij����ú���![]() �Ĵ���ʽ��ʾ���������
�Ĵ���ʽ��ʾ���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() Ϊ��ֵʱ���߶�
Ϊ��ֵʱ���߶�![]() ���M���У�
���M����
��3������M���߶�![]() ֻ��һ�������㣬��
ֻ��һ�������㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�������BF=![]() t��0��t��8����������t=
t��0��t��8����������t=![]() ��������0��t��
��������0��t��![]() ��
��![]() ��t��8
��t��8
��������
��1������MB=MF��AB=AD���Ƴ�MF��AD����ƽ���߷��߶γɱ����ɵ�![]() �������BF�ij���
�������BF�ij���
��2�����߶�EN���M����ʱ����֪��BEN�ס�BOA���ٸ��ݶ�Ӧ�߳ɱ�����⼴�ɣ�
��3�����ݻ�ͼ��֪����0��t��![]() ʱ����M���߶�ENֻ��һ�������㣬��F��N�غϺ��M���߶�ENֻ��һ�������㣬���F��N�غ�ʱt��ֵ���ɣ�
ʱ����M���߶�ENֻ��һ�������㣬��F��N�غϺ��M���߶�ENֻ��һ�������㣬���F��N�غ�ʱt��ֵ���ɣ�
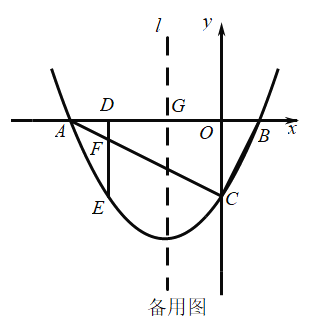
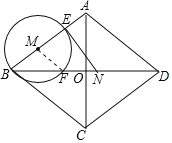
��1������MF����ͼ��
![]()
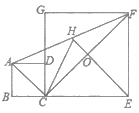
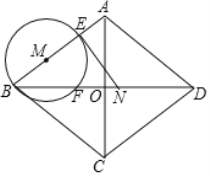
���ı���ABCD�����Σ�
��AB=AD��AC��BD��OA=OC=6��OB=OD=8��
��Rt��AOB��![]() ��
��
��MB=MF��AB=AD��
���ABD=��ADB=��MFB��
��MF��AD��
��![]() ,
,
��![]() ,
,
��BF=![]() t��0��t��8��.
t��0��t��8��.
��2�����߶�EN���M����ʱ����֪��BEN�ס�BOA��
��![]() ��
��
��![]() ��
��
��t=![]() ��
��
��t=![]() sʱ���߶�EN���M����.
sʱ���߶�EN���M����.
��3���ٸ����������֪������0��t��![]() ʱ����M���߶�ENֻ��һ��������.
ʱ����M���߶�ENֻ��һ��������.
�ڵ�F��N�غ�ʱ������![]() t+2t=16������ó�t=
t+2t=16������ó�t=![]() ��
��
����ͼ�����֪����![]() ��t��8ʱ����M���߶�ENֻ��һ��������.
��t��8ʱ����M���߶�ENֻ��һ��������.
������������0��t��![]() ��
��![]() ��t��8ʱ����M���߶�ENֻ��һ�������㣮
��t��8ʱ����M���߶�ENֻ��һ�������㣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�