ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЃx2ЃЋbxЃЋcгыxжсЯрНЛгкAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
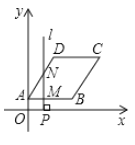
ЃЈ2ЃЉдкЕкЖўЯѓЯоФкШЁвЛЕуCЃЌзїCDДЙжБxжсгкЕуDЃЌСДНгACЃЌЧвADЃН5ЃЌCDЃН8ЃЌНЋRtЁїACDбиxжсЯђгвЦНвЦmИіЕЅЮЛЃЌЕБЕуCТфдкХзЮяЯпЩЯЪБЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЕуCЕквЛДЮТфдкХзЮяЯпЩЯМЧЮЊЕуEЃЌЕуPЪЧХзЮяЯпЖдГЦжсЩЯвЛЕуЃЎЪдЬНОПЃКдкХзЮяЯпЩЯЪЧЗёДцдкЕуQЃЌЪЙвдЕуBЁЂEЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃНЃx2ЃЋ4xЃЋ5ЃЈ2ЃЉmЕФжЕЮЊ7Лђ9ЃЈ3ЃЉQЕуЕФзјБъЮЊЃЈЉ2ЃЌЉ7ЃЉЛђЃЈ6ЃЌЉ7ЃЉЛђЃЈ4ЃЌ5ЃЉ
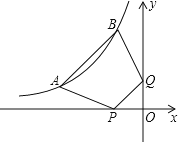
ЁОНтЮіЁПЪдЬтЃЈ1ЃЉгЩAЁЂBЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉгЩЬтвтПЩЧѓЕУCЕузјБъЃЌЩшЦНвЦКѓЕФЕуCЕФЖдгІЕуЮЊCЁфЃЌдђCЁфЕуЕФзнзјБъЮЊ8ЃЌДњШыХзЮяЯпНтЮіЪНПЩЧѓЕУCЁфЕуЕФзјБъЃЌдђПЩЧѓЕУЦНвЦЕФЕЅЮЛЃЌПЩЧѓЕУmЕФжЕЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩЧѓЕУEЕузјБъЃЌСЌНгBEНЛЖдГЦжсгкЕуMЃЌЙ§EзїEFЁЭxжсгкЕуFЃЌЕБBEЮЊЦНааЫФБпаЮЕФБпЪБЃЌЙ§QзїЖдГЦжсЕФДЙЯпЃЌДЙзуЮЊNЃЌдђПЩжЄЕУЁїPQNЁеЁїEFBЃЌПЩЧѓЕУQNЃЌМДПЩЧѓЕУQЕНЖдГЦжсЕФОрРыЃЌдђПЩЧѓЕУQЕуЕФКсзјБъЃЌДњШыХзЮяЯпНтЮіЪНПЩЧѓЕУQЕузјБъЃЛЕБBEЮЊЖдНЧЯпЪБЃЌгЩBЁЂEЕФзјБъПЩЧѓЕУЯпЖЮBEЕФжаЕузјБъЃЌЩшQЃЈxЃЌyЃЉЃЌгЩPЕуЕФКсзјБъдђПЩЧѓЕУQЕуЕФКсзјБъЃЌДњШыХзЮяЯпНтЮіЪНПЩЧѓЕУQЕуЕФзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯпy=Љx2+bx+cгыxжсЗжБ№НЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉСНЕуЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊy=Љx2+4x+5ЃЛ
ЃЈ2ЃЉЁпAD=5ЃЌЧвOA=1ЃЌ
ЁрOD=6ЃЌЧвCD=8ЃЌ
ЁрCЃЈЉ6ЃЌ8ЃЉЃЌ
ЩшЦНвЦКѓЕФЕуCЕФЖдгІЕуЮЊCЁфЃЌдђCЁфЕуЕФзнзјБъЮЊ8ЃЌ
ДњШыХзЮяЯпНтЮіЪНПЩЕУ8=Љx2+4x+5ЃЌНтЕУx=1Лђx=3ЃЌ
ЁрCЁфЕуЕФзјБъЮЊЃЈ1ЃЌ8ЃЉЛђЃЈ3ЃЌ8ЃЉЃЌ
ЁпCЃЈЉ6ЃЌ8ЃЉЃЌ
ЁрЕБЕуCТфдкХзЮяЯпЩЯЪБЃЌЯђгвЦНвЦСЫ7Лђ9ИіЕЅЮЛЃЌ
ЁрmЕФжЕЮЊ7Лђ9ЃЛ
ЃЈ3ЃЉЁпy=Љx2+4x+5=ЉЃЈxЉ2ЃЉ2+9ЃЌ
ЁрХзЮяЯпЖдГЦжсЮЊx=2ЃЌ
ЁрПЩЩшPЃЈ2ЃЌtЃЉЃЌ
гЩЃЈ2ЃЉПЩжЊEЕузјБъЮЊЃЈ1ЃЌ8ЃЉЃЌ
ЂйЕБBEЮЊЦНааЫФБпаЮЕФБпЪБЃЌСЌНгBEНЛЖдГЦжсгкЕуMЃЌЙ§EзїEFЁЭxжсгкЕуFЃЌЕБBEЮЊЦНааЫФБпаЮЕФБпЪБЃЌЙ§QзїЖдГЦжсЕФДЙЯпЃЌДЙзуЮЊNЃЌШчЭМЃЌ
дђЁЯBEF=ЁЯBMP=ЁЯQPNЃЌ
дкЁїPQNКЭЁїEFBжа

ЁрЁїPQNЁеЁїEFBЃЈAASЃЉЃЌ
ЁрNQ=BF=OBЉOF=5Љ1=4ЃЌ
ЩшQЃЈxЃЌyЃЉЃЌдђQN=|xЉ2|ЃЌ
Ёр|xЉ2|=4ЃЌНтЕУx=Љ2Лђx=6ЃЌ
ЕБx=Љ2Лђx=6ЪБЃЌДњШыХзЮяЯпНтЮіЪНПЩЧѓЕУy=Љ7ЃЌ
ЁрQЕузјБъЮЊЃЈЉ2ЃЌЉ7ЃЉЛђЃЈ6ЃЌЉ7ЃЉЃЛ
ЂкЕБBEЮЊЖдНЧЯпЪБЃЌ
ЁпBЃЈ5ЃЌ0ЃЉЃЌEЃЈ1ЃЌ8ЃЉЃЌ
ЁрЯпЖЮBEЕФжаЕузјБъЮЊЃЈ3ЃЌ4ЃЉЃЌдђЯпЖЮPQЕФжаЕузјБъЮЊЃЈ3ЃЌ4ЃЉЃЌ
ЩшQЃЈxЃЌyЃЉЃЌЧвPЃЈ2ЃЌtЃЉЃЌ
Ёрx+2=3ЁС2ЃЌНтЕУx=4ЃЌАбx=4ДњШыХзЮяЯпНтЮіЪНПЩЧѓЕУy=5ЃЌ
ЁрQЃЈ4ЃЌ5ЃЉЃЛ
злЩЯПЩжЊQЕуЕФзјБъЮЊЃЈЉ2ЃЌЉ7ЃЉЛђЃЈ6ЃЌЉ7ЃЉЛђЃЈ4ЃЌ5ЃЉЃЎ