题目内容
【题目】正方形
、
、
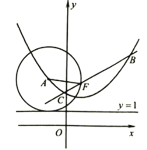
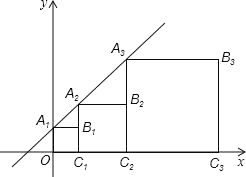
、…按如图所示的方式放置，点
、
、
、…和点
、
、
、…分别在直线
和
轴上，则点
的坐标是__________．（答案不需要化简）
【答案】(
，
)
【解析】
根据一次函数图象上点的坐标特征可得出点
的坐标，结合正方形的性质可得出点
的坐标，同理得出
的坐标，再得出
的坐标，以此类推，根据点的坐标变化找出
的坐标，由此即可得出答案.
当
时，
，
∴点的坐标为(0，1)，
∵四边形
为正方形，
∴点的坐标为(1，1)，
当
时，
，
∴点的坐标为(1，2)，
∵四边形
为正方形，
∴点的坐标为(3，2)，
同理可得：点
的坐标为(3，4)，点
的坐标为(7，4)，点
的坐标为(7，8)，点
的坐标为(15，8)，……
∴点的坐标为(
，
)，
∴点
的(，)，
故答案为：(，).
练习册系列答案
名校课堂系列答案
相关题目
