题目内容
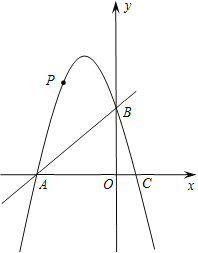
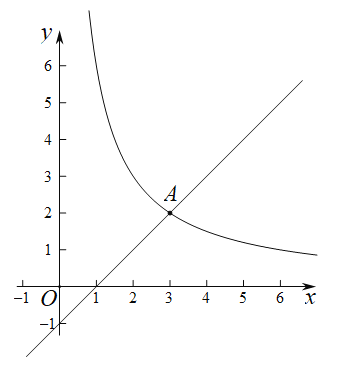
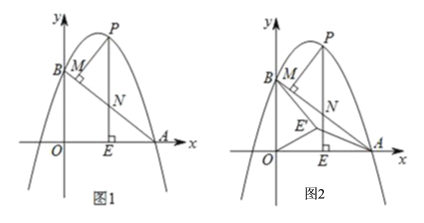
【题目】如图1,抛物线y=ax2﹣6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求出抛物线的函数表达式;
(2)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
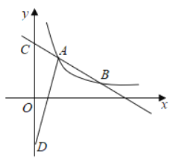
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为30°,连接E'A、E'B,在坐标平面内找一点Q,使△AOE′~△BOQ,并求出Q的坐标.
【答案】(1)y=-![]() x2+
x2+![]() x+6;(2)m=4;(3)Q1(
x+6;(2)m=4;(3)Q1(![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() ).
).
【解析】
(1)把点A(8,0)代入抛物线解析式求解即得;
(2)易求得直线AB解析式为y=![]() x+6,再证明△ANE∽△PNM,由相似三角形的性质得
x+6,再证明△ANE∽△PNM,由相似三角形的性质得![]() ,由E(m,0)(0<m<8)可得P(m,
,由E(m,0)(0<m<8)可得P(m,![]() ),N(m,
),N(m,![]() m+6),然后用m的代数式表示出AN和PN,解方程即可;
m+6),然后用m的代数式表示出AN和PN,解方程即可;
(3)由题意可求得OQ的长,过点Q作QH⊥y轴于H,然后利用∠BOQ=∠AOE′=30°,可求得QH和OH的长,进一步即得结果.
解:(1)把A(8,0)代入y=ax2﹣6ax+6,得64a﹣48a+6=0,解得a=![]() ,
,
∴抛物线的函数表达式为:y=![]() x2+
x2+![]() x+6;
x+6;
(2)如图1,在y=![]() x2+
x2+![]() x+6中,令x=0,得y=6,∴B(0,6),
x+6中,令x=0,得y=6,∴B(0,6),
设直线AB解析式为y=kx+b,则![]() ,解得
,解得 ,
,
∴直线AB解析式为y=![]() x+6
x+6
∵PE⊥x轴,PM⊥AB
∴∠AEN=∠PMN=90°,
∵∠ANE=∠PNM,∴△ANE∽△PNM.
∴![]() ,
,![]() ,
,
∵S1:S2=36:25,

∴![]() ,
,
∴6AN=5PN
∵E(m,0)(0<m<8),∴OE=m,AE=8﹣m,
∴P(m,![]() ),N(m,
),N(m,![]() m+6),
m+6),
∴EN=![]() m+6,PN=PE﹣EN=
m+6,PN=PE﹣EN=![]() ﹣(
﹣(![]() m+6)=
m+6)=![]() +3m,
+3m,
∵AB=![]() =10
=10
∴cos∠OAB=![]() ,即
,即![]() ,
,
∴AN=![]() (8﹣m),
(8﹣m),
∴6×![]() (8﹣m)=5×(
(8﹣m)=5×(![]() +3m),解得:m1=4,m2=8(不符合题意,舍去),
+3m),解得:m1=4,m2=8(不符合题意,舍去),
∴m=4;
(3)如图2,∵线段OE绕点O逆时针旋转得到OE′,旋转角为30°,
∴OE′=OE=4,∠AOE′=30°
∵△AOE′∽△BOQ,
∴![]() ,∠BOQ=∠AOE′=30°,
,∠BOQ=∠AOE′=30°,
∴![]() ,即OQ=3,
,即OQ=3,
过点Q作QH⊥y轴于H,
∴QH=![]() OQ=
OQ=![]() ,OH=
,OH=![]() ,
,
∴当点Q在y轴右侧时,Q1(![]() ,
,![]() ),
),
当点Q在y轴左侧时,Q2(﹣![]() ,
,![]() ).
).
综上所述,Q的坐标为:Q1(![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() ).
).


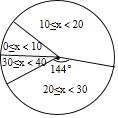
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.