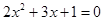题目内容
已知关于x的一元二次方程x2-2 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.
⑴求实数m的最大整数值;
⑵在⑴的条下,方程的实数根是x1,x2,求代数式x12+x22-x1x2的值.
 x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.⑴求实数m的最大整数值;
⑵在⑴的条下,方程的实数根是x1,x2,求代数式x12+x22-x1x2的值.
⑴m的最大整数值为m=1
(2)x12+x22-x1x2= 5
(2)x12+x22-x1x2= 5
试题分析:一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.根据一元二次方程的根的判别式,建立关于m的不等式,求出m的取值范围.
试题解析:⑴由题意,得:△>0,即:
 >0 解得 m<2,∴m的最大整数值为m="1"
>0 解得 m<2,∴m的最大整数值为m="1" 把m=1代入关于x的一元二次方程x2-2
 x+m=0得x2-2
x+m=0得x2-2 x+1=0,
x+1=0,根据根与系数的关系:x1+x2 =2
 , x1x2=1,
, x1x2=1,∴x12+x22-x1x2= (x1+x2)2-3x1x2=(2
 )2-3×1=5
)2-3×1=5
练习册系列答案
相关题目

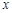 的方程
的方程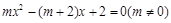 .
. 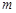 的值.
的值.



 且
且
 且m≠0
且m≠0 (2)
(2)