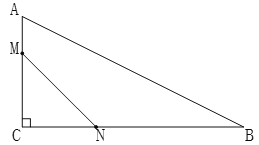
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 方向向
方向向![]() 点运动,动点
点运动,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 方向向
方向向![]() 点运动,如果
点运动,如果![]() ,
,![]() 两点同时出发,当
两点同时出发,当![]() 到达
到达![]() 点处时,两点都停止运动.设运动的时间为
点处时,两点都停止运动.设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() .
.
(1)用含![]() 的代数式表示:
的代数式表示:
![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)根据“路程=速度![]() 时间”可求得AM和CN的长,再根据线段的和差可得CM的长,最后根据直角三角形的面积公式即可得S的值;
时间”可求得AM和CN的长,再根据线段的和差可得CM的长,最后根据直角三角形的面积公式即可得S的值;
(2)由题(1)的结论知S是关于t的二次函数,先求出t的取值范围,再利用二次函数的性质求解即可.
(1)由题意得:![]() ,
,![]()
![]()
![]()
![]() ;
;
(2)由M、N两点的运动路径得:![]()
但当![]() 和
和![]() 时,M、C、N三点不能构成三角形,故
时,M、C、N三点不能构成三角形,故![]()
![]()
由二次函数的性质可知:当![]() 时,S随t的增大而增大;当
时,S随t的增大而增大;当![]() 时,S随t的增大而减小
时,S随t的增大而减小
则当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.

练习册系列答案
相关题目