题目内容
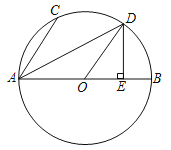
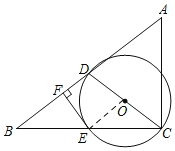
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O交BC于点E,过点E作EF⊥AB于点F.
(1)判断EF所在直线与⊙O的位置关系,并说明理由.
(2)若∠B=40°,⊙O的半径为6,求![]() 的长.(结果保留π)
的长.(结果保留π)

【答案】(1)EF与⊙O相切,理由见解析;(2)![]()
【解析】
(1)如图,连接OE,根据直角三角形的性质得到CD=BD,得到∠DBC=∠DCB,根据等腰三角形的性质得到∠OEC=∠OCE,得到∠OEC=∠DBC,推出∠OEF=90°,于是得到结论;
(2)根据弧长公式计算.
(1)EF所在直线与⊙O相切.
如图,连结OE.
∵∠ACB=90°,D为AB的中点,
∴BD=CD.
∴∠B=∠DCB.
∵OE=OC,
∴∠OEC=∠OCE.
∴∠OEC=∠B.
∴OE∥DB.
∴∠OEF=∠BFE.
∵EF⊥AB,
∴∠BFE=90°.
∴∠OEF=90°.
∵点E在⊙O上,∴EF与⊙O相切.
(2)∵∠OCE+∠OEC+∠EOC=180°,
∠OCE=∠OEC=∠B=40°,
∴∠EOC=180°﹣∠OCE﹣∠OEC=180°﹣40°﹣40°=100°.
∴![]() 的长
的长![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目