题目内容
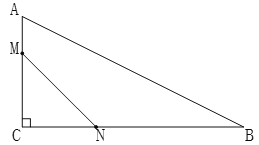
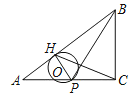
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,P是AC上的一点,PH⊥AB于点H,以PH为直径作⊙O,当CH与PB的交点落在⊙O上时,AP的值为( )
A.![]() B.
B.![]() C.2D.3
C.2D.3
【答案】A
【解析】
当CH与PB的交点D落在⊙O上时,因为HP是直径,可以判定BP⊥HC,再证BP垂直平分HC,求出BH的长度,最后证△AHP∽△ACB,即可求出AP的长度.
解:如图所示,当CH与PB的交点D落在⊙O上时,

∵HP是直径,
∴∠HDP=90°,
∴BP⊥HC,
∴∠HDP=∠BDH=90°,
又∵∠PHD+∠BHD=90°,∠BHD+∠HBD=90°,
∴∠PHD=∠HBD,
∴△PHD∽△HBD,
![]()
∴HD2=PDBD,
同理可证CD2=PDBD,
∴HD=CD,
∴BD垂直平分CH,
∴BH=BC=3,
在Rt△ACB中,
AB=![]()
∴AH=5﹣3=2,
∵∠A=∠A,∠AHP=∠ACB=90°,
∴△AHP∽△ACB,
![]()
![]()
∴AP=![]() ,
,
故选:A.

练习册系列答案
相关题目
【题目】在硬地上抛掷一枚图钉,通常会出现两种情况:

下面是小明和同学做“抛掷图钉实验”获得的数据:
抛掷次数n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
针尖不着地的频数m | 63 | 120 | 186 | 252 | 310 | 360 | 434 | 488 | 549 | 610 |
针尖不着地的频率 | 0.63 | 0.60 | 0.63 | 0.60 | 0.62 | 0.61 |
(1)填写表中的空格;
(2)画出该实验中,抛掷图钉钉尖不着地频率的折线统计图;

(3)根据“抛掷图钉实验”的结果,估计“钉尖着地”的概率为 .