Question

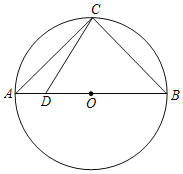
【题目】如图，AB为⊙O的直径，点C、D都在⊙O上，且CD平分∠ACB，交AB于点E．

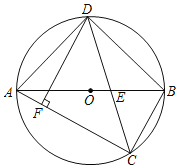
（1）求证：∠ABD＝∠BCD；

（2）若DE＝13，AE＝17，求⊙O的半径；

（3）DF⊥AC于点F，试探究线段AF、DF、BC之间的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）12；（3）AF+BC＝DF，理由见解析

【解析】

（1）由CD平分∠ACB，根据圆周角定理，可得∠ACD＝∠BCD＝∠ABD；

（2）过点E作EM⊥AD于点M，求出AD长，则AB＝AD，可求出AB,则答案得出；

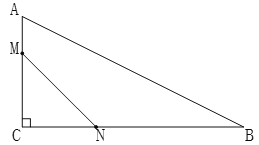
（3）过点D作DN⊥CB，交CB的延长线于点N，可证明△DAF≌△DBN，则AF＝BN，DF＝CF则结论AF+BC＝DF可得出．

（1）证明：∵CD平分∠ACB，

∴∠ACD＝∠BCD，

∵∠ACD＝∠ABD，

∴∠ABD＝∠BCD；

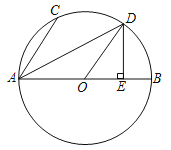
（2）解：如图1，过点E作EM⊥AD于点M，

∵AB为⊙O的直径，

∴∠ACB＝90°，∠ADB＝90°，

∴∠DAB＝∠BCD＝45°，

∵AE＝17，

∴ME＝AM＝17×＝，

∵DE＝13，

∴DM＝

∴AD＝AM+DM＝，

∴AB＝AD＝

∴AO＝＝12；

（3）AF+BC＝DF．理由如下：

如图2，过点D作DN⊥CB，交CB的延长线于点N，

∵四边形DACB内接于圆，

∴∠DBN＝∠DAF，

∵DF⊥AC，DN⊥CB，CD平分∠ACB，

∴∠AFD＝∠DNB＝90°，DF＝DN，

∴△DAF≌△DBN（AAS），

∴AF＝BN，CF＝CN，

∵∠FCD＝45°，

∴DF＝CF，

∴CN＝BN+BC＝AF+BC＝DF．

即AF+BC＝DF．