题目内容
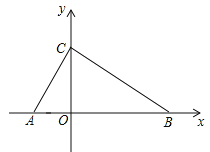
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
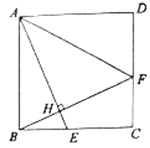
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2-4x+3.(2)当m=![]() 时,四边形AOPE面积最大,最大值为
时,四边形AOPE面积最大,最大值为![]() .(3)P点的坐标为 :P1(
.(3)P点的坐标为 :P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ).
).
【解析】
(1)利用对称性可得点D的坐标,利用交点式可得抛物线的解析式;
(2)设P(m,m2-4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得四边形AOPE的面积,利用配方法可得其最大值;
(3)存在四种情况:
如图3,作辅助线,构建全等三角形,证明△OMP≌△PNF,根据OM=PN列方程可得点P的坐标;同理可得其他图形中点P的坐标.
(1)如图1,设抛物线与x轴的另一个交点为D,
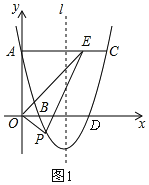
由对称性得:D(3,0),
设抛物线的解析式为:y=a(x-1)(x-3),
把A(0,3)代入得:3=3a,
a=1,
∴抛物线的解析式;y=x2-4x+3;
(2)如图2,设P(m,m2-4m+3),
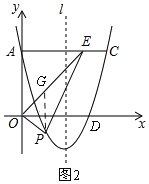
∵OE平分∠AOB,∠AOB=90°,
∴∠AOE=45°,
∴△AOE是等腰直角三角形,
∴AE=OA=3,
∴E(3,3),
易得OE的解析式为:y=x,
过P作PG∥y轴,交OE于点G,
∴G(m,m),
∴PG=m-(m2-4m+3)=-m2+5m-3,
∴S四边形AOPE=S△AOE+S△POE,
=![]() ×3×3+
×3×3+![]() PGAE,
PGAE,
=![]() +
+![]() ×3×(-m2+5m-3),
×3×(-m2+5m-3),
=-![]() m2+
m2+![]() m,
m,
=![]() (m-
(m-![]() ,
,
∵-![]() <0,
<0,
∴当m=![]() 时,S有最大值是
时,S有最大值是![]() ;
;
(3)如图3,过P作MN⊥y轴,交y轴于M,交l于N,
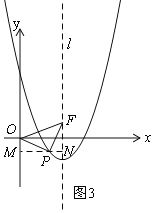
∵△OPF是等腰直角三角形,且OP=PF,
易得△OMP≌△PNF,
∴OM=PN,
∵P(m,m2-4m+3),
则-m2+4m-3=2-m,
解得:m=![]() 或
或![]() ,
,
∴P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
如图4,过P作MN⊥x轴于N,过F作FM⊥MN于M,
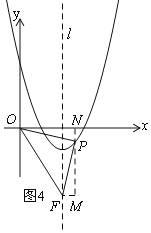
同理得△ONP≌△PMF,
∴PN=FM,
则-m2+4m-3=m-2,
解得:x=![]() 或
或![]() ;
;
P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上所述,点P的坐标是:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案