��Ŀ����
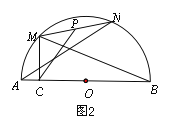
����Ŀ����ͼ����O��ֱ��AB��26��P��AB�ϣ������A��B�غϣ�����һ�㣬��C��DΪ��O�ϵ����㣮����APD����BPC����ơ�DPCΪֱ��AB��������������
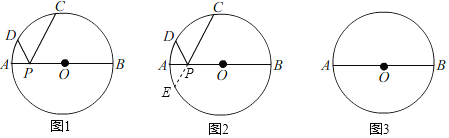
��1������BPC����DPC��60�������DPC��ֱ��AB�������������𣿲�˵�����ɣ�
��2���������������DPC�Ķ����뻡CD�Ķ����Ĺ�ϵ������֤������ʾ���ӳ�CP����O�ڵ�E����
��3����ֱ��AB������������Ϊ120�����ҡ�PCD���ܳ�Ϊ24+13![]() ��ֱ��д��AP�ij���
��ֱ��д��AP�ij���
���𰸡���1����DPC��ֱ��AB�Ļ����ǣ����ɼ���������2��������������CPD�Ķ�����![]() �Ķ�����֤������������3��3��23��
�Ķ�����֤������������3��3��23��
��������
��1���ɡ�BPC����DPC��60�����ƽ�ǣ�180�������������APD��60������BPC��������˵����DPC��ֱ��AB�Ļ����ǣ�
��2���ӳ�CP��ԲO�ڵ�E������OD��OC��OE���������������Ķ����϶Զ�����ȣ��ɵó���APE����APD����Բ�ĶԳ��Կɵó���E����D���ɵ��������ε����ʿɵó���E����C�������ɵó���D����C�������������ڽǺͶ����ɵó���COD����CPD����������������CPD�Ķ�����![]() �Ķ�����
�Ķ�����
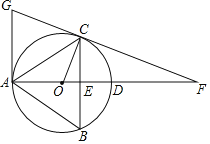
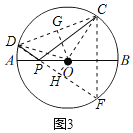
��3���ٵ���P�ڰ뾶OA��ʱ����ͼ3�У�����F��CF��AB����ԲO�ڵ�F������PF����PF��PC�����ã�2���ķ����ɵó���P��D��F��ͬһ��ֱ���ϣ���ֱ��AB������������Ϊ120�����ɵó���APD����BPC��30���������ɵó���CPF��60��������PFC�ǵȱ������Σ����ݵȱ������ε����ʿɵó���CFD��60��������OC��OD������O��OG��CD�ڵ�G�����COD��120�������ݵ��������ε����ʿɵó�CD��2DG����DOG��![]() ��COD��60�������Բ��ֱ��Ϊ26�ɵó�CD��13
��COD��60�������Բ��ֱ��Ϊ26�ɵó�CD��13![]() ���ɡ�PCD���ܳ�Ϊ24+13
���ɡ�PCD���ܳ�Ϊ24+13![]() ���ɵó�DF��24������O��OH��DF�ڵ�H����Rt��OHD����Rt��OHD�У�ͨ����ֱ�������οɵó�OH��OP��ֵ���ٸ���AP��OA��OP�����AP��ֵ���ڵ���P�ڰ뾶OB��ʱ���âٵķ������ɵã�BP��3���ٸ���AP��AB��BP�����AP��ֵ�����ϼ��ɵó����ۣ�
���ɵó�DF��24������O��OH��DF�ڵ�H����Rt��OHD����Rt��OHD�У�ͨ����ֱ�������οɵó�OH��OP��ֵ���ٸ���AP��OA��OP�����AP��ֵ���ڵ���P�ڰ뾶OB��ʱ���âٵķ������ɵã�BP��3���ٸ���AP��AB��BP�����AP��ֵ�����ϼ��ɵó����ۣ�
��1���ߡ�BPC����DPC��60����
���APD��180������BPC����DPC��180����60����60����60����
���APD����BPC��
���DPC��ֱ��AB�Ļ����ǣ�
��2��������������CPD�Ķ�����![]() �Ķ������������£�
�Ķ������������£�
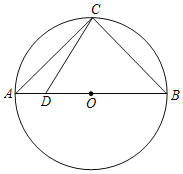
��ͼ2���ӳ�CP��ԲO�ڵ�E������OD��OC��OE��

�ߡ�CPB����APE����APD����CPB��
���APE����APD��
��Բ����Գ�ͼ�Σ�
���E����D��
��OE��OC��
���E����C��
���D����C��
���������ڽǺͶ�������֪����COD����CPD��
��������������CPD�Ķ�����![]() �Ķ�����
�Ķ�����
��3���ٵ���P�ڰ뾶OA��ʱ����ͼ3�У�����F��CF��AB����ԲO�ڵ�F������PF����PF��PC��
ͬ��2���ķ����ɵã���P��D��F��ͬһ��ֱ���ϣ�
��ֱ��AB������������Ϊ120����
���APD����BPC��30����
���CPF��60����
���PFC�ǵȱ������Σ�
���CFD��60����
����OC��OD������O��OG��CD�ڵ�G�����COD��120����
��CD��2DG����DOG��![]() ��COD��60����
��COD��60����
��AB=26��
��OC=13��
��![]()
��CD��2��![]() ��
��![]() .
.
�ߡ�PCD���ܳ�Ϊ24+![]() ��
��
��PD+PC+CD��24+![]() ��
��
��PD+PC��DF��24��
����O��OH��DF�ڵ�H����DH��FH��![]() DF��12��
DF��12��
��Rt��OHD��OH��![]() ,
,
��Rt��OHP����OPH��30����
��OP��2OH��10��
��AP��OA��OP��13��10��3��
�ڵ���P�ڰ뾶OB��ʱ��
ͬ�ٵķ������ɵã�BP��3��
��AP��AB��BP��26��3��23��
����������AP�ij���3��23��

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�