题目内容
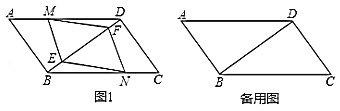
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,
重合,![]() 为折痕,则
为折痕,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
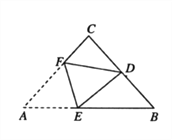
【解析】先根据翻折变换的性质得到△DEF≌△AEF,再根据等腰三角形的性质及三角形外角的性质可得到∠BED=CDF,设CD=1,CF=x,则CA=CB=2,再根据勾股定理即可求出x的值,利用三角函数的定义求出sin∠BED=sin∠CDF的值.
∵△DEF是△AEF翻折而成,
∴△DEF≌△AEF,
∴∠A=∠EDF,DF=FA,
∵△ABC是等腰直角三角形,
∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,
∴∠BED=∠CDF,
设CD=1,CF=x,则CA=CB=2,
∴DF=FA=2-x,
∴在Rt△CDF中,由勾股定理得,CF2+CD2=DF2,即x2+1=(2-x)2,
解得x=![]() ,
,
∴sin∠BED=sin∠CDF=![]() .
.
故选B.

练习册系列答案
相关题目