Question

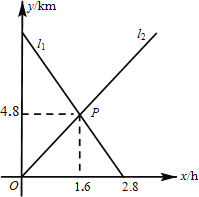
【题目】已知，如图点A（1，1），B（2，﹣3），点P为x轴上一点，当|PA﹣PB|最大时，点P的坐标为（　　）

A. （﹣1，0） B. （，0） C. （，0） D. （1，0）

Answer 1

【答案】B

【解析】

作A关于x轴对称点C，连接BC并延长，BC的延长线与x轴的交点即为所求的P点；首先利用待定系数法即可求得直线BC的解析式，继而求得点P的坐标．

作A关于x轴对称点C，连接BC并延长交x轴于点P，

∵A（1，1），

∴C的坐标为（1，﹣1），

连接BC，

设直线BC的解析式为：y＝kx+b，

∴，

解得：，

∴直线BC的解析式为：y＝﹣2x+1，

当y＝0时，x＝，

∴点P的坐标为：（，0），

∵当B，C，P不共线时，根据三角形三边的关系可得：|PA﹣PB|＝|PC﹣PB|＜BC，

∴此时|PA﹣PB|＝|PC﹣PB|＝BC取得最大值．

故选：B．