题目内容
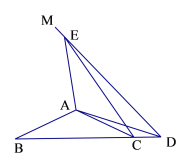
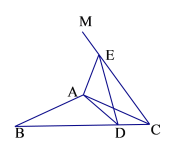
【题目】如图所示的网格是正方形网格,则∠PAB﹣∠PCD=_____°.(点A,B,C,D,P是网格线交点)
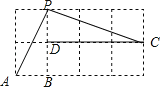
【答案】45
【解析】
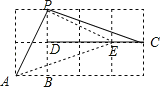
连接AE,PE,由图可知,∠EAB=∠PCD,则∠PAB∠PCD=∠PAB∠EAB=∠PAE,然后根据勾股定理可以求得PA、PE、AE的长,再利用勾股定理的逆定理可以判断△PAE的形状,从而可以得到∠PAE的度数,然后即可得到∠PAB∠PCD的度数.
解:连接AE,PE,
则∠EAB=∠PCD,
故∠PAB﹣∠PCD=∠PAB﹣∠EAB=∠PAE,
设正方形网格的边长为a,
则PA=![]() ,PE=
,PE=![]() ,AE=
,AE=![]() ,
,
∵PA2+PE2=5a2+5a2=10a2=AE2,
∴△APE是直角三角形,∠APE=90°,
又∵PA=PE,
∴∠PAE=∠PEA=45°,
∴∠PAB﹣∠PCD=45°,
故答案为:45.

练习册系列答案
相关题目
【题目】有这样一个问题:探究函数![]() 的图象与性质并解决问题.
的图象与性质并解决问题.
小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)取几组![]() 与
与![]() 的对应值,填写在下表中.
的对应值,填写在下表中.
| … |
|
|
| 0 | 1 | 1.2 | 1.25 | 2.75 | 2.8 | 3 | 4 | 5 | 6 | 8 | … |
| … | 1 | td style="width:6%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.62pt; vertical-align:middle">2 | 3 | 6 | 7.5 | 8 | 8 | 7.5 | 6 | 3 |
| 1.5 | 1 | … |
![]() 的值为_____________;
的值为_____________;
(3)如下图,在平面直角坐标系![]() 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
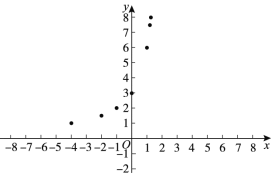
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数![]() 的图象是轴对称图形,它的对称轴是____________;
的图象是轴对称图形,它的对称轴是____________;
②过点![]() 作直线
作直线![]() 轴,与函数
轴,与函数![]() 的图象交于点
的图象交于点![]() (点
(点![]() 在点
在点![]() 的左侧),则
的左侧),则![]() 的值为____________.
的值为____________.