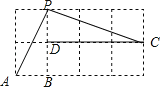Question

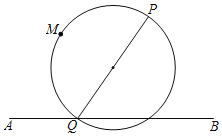
【题目】如图，平面上存在点P、点M与线段AB．若线段AB上存在一点Q，使得点M在以PQ为直径的圆上，则称点M为点P与线段AB的共圆点．

已知点P（0，1），点A（﹣2，﹣1），点B（2，﹣1）．

（1）在点O（0，0），C（﹣2，1），D（3，0）中，可以成为点P与线段AB的共圆点的是　 　；

（2）点K为x轴上一点，若点K为点P与线段AB的共圆点，请求出点K横坐标xK的取值范围；

（3）已知点M（m，﹣1），若直线y＝x+3上存在点P与线段AM的共圆点，请直接写出m的取值范围．

Answer 1

【答案】（1）C；（2）﹣1﹣≤xk≤1﹣或﹣1≤xk≤1+；（3）m≤3﹣2或m≥3+2．

【解析】

（1）由题意可知当Q与A重合时，点C在以AP为直径的圆上，所以可以成为点P与线段AB的共圆点的是C；

（2）根据题意由两点的距离公式可得AP=BP=2，分别画以AP和BP为直径的圆交x轴于4个点：K1、K2、K3、K4，结合图形2可得4个点的坐标，从而得结论；

（3）由题意先根据直线y=x+3，当x=0和y=0计算与x轴和y轴的交点坐标，分两种情况：M在A的左侧和右侧，先计算圆E与直线y=x+3相切时m的值，从而根据图形可得结论．

解：（1）如图1，可以成为点P与线段AB的共圆点的是C，

故答案为：C；

（2）∵P（0，1），点A（﹣2，﹣1），点B（2，﹣1）．

∴AP＝BP＝＝2，

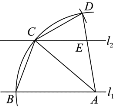
如图2，分别以PA、PB为直径作圆，交x轴于点K1、K2、K3、K4，

∵OP＝OG＝1，OE∥AB，

∴PE＝AE＝，

∴OE＝AG＝1，

∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），

∵点K为点P与线段AB的共圆点，

∴﹣1﹣≤xk≤1﹣或﹣1≤xk≤1+；

（3）分两种情况：

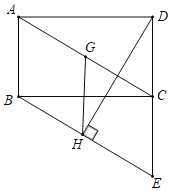
①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝x+3相切于点F，连接EF，则EF⊥FH，

当x＝0时，y＝3，当y＝0时，y＝x+3＝0，x＝﹣6，

∴ON＝3，OH＝6，

∵tan∠EHF＝＝＝，

设EF＝a，则FH＝2a，EH＝a，

∴OE＝6﹣a，

Rt△OEP中，OP＝1，EP＝a，

由勾股定理得：EP2＝OP2+OE2，

∴，

解得：a＝（舍去）或，

∴QG＝2OE＝2（6﹣a）＝﹣3+2，

∴m≤3﹣2；

②如图4，当M在点A的右侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝x+3相切于点F，连接EF，则EF⊥FH，

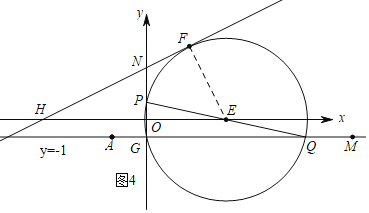
同理得QG＝3+2，

∴m≥3+2，

综上，m的取值范围是m≤3﹣2或m≥3+2．