题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
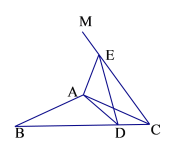
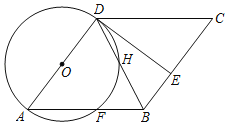
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
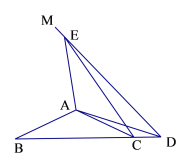
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)∠ADE=30°,理由详见解析;(2)(1)中的结论成立,证明详见解析;(3)![]()
【解析】
(1)利用SAS定理证明△ABD≌△ACE,根据相似三角形的性质得到AD=AE,∠CAE=∠BAD,根据等腰三角形的性质、三角形内角和定理计算即可证明;
(2)同(1)的证明方法相同;
(3)证明△ADF∽△ACD,根据相似三角形的性质得到AF=![]() ,求出AD的最小值,得到AF的最小值,求出CF的最大值.
,求出AD的最小值,得到AF的最小值,求出CF的最大值.
解:(1)∠ADE=30![]() .
.
理由如下:∵AB=AC,∠BAC=120![]() ,∴∠ABC=∠ACB=30
,∴∠ABC=∠ACB=30![]() ,
,
∵∠ACM=∠ACB,∴∠ACM=∠ABC,
在△ABD和△ACE中,
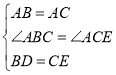 ,
,
∴△ABD≌△ACE,
∴AD=AE,∠CAE=∠BAD,
∴∠DAE=∠BAC=120![]() ,
,
∴∠ADE=30![]() ;
;
(2)(1)中的结论成立,
证明:∵∠BAC=120![]() ,AB=AC,
,AB=AC,
∴∠B=∠ACB=30![]() .
.
∵∠ACM=∠ACB,
∴∠B=∠ACM=30![]() .
.
在△ABD和△ACE中,
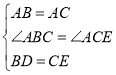 ,
,
∴△ABD≌△ACE.
∴AD=AE,∠BAD=∠CAE.
∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=120![]() .即∠DAE=120
.即∠DAE=120![]() .
.
∵AD=AE,
∴∠ADE=∠AED=30![]() ;
;
(3)∵AB=AC,AB=6,
∴AC=6,
∵∠ADE=∠ACB=30![]() 且∠DAF=∠CAD,
且∠DAF=∠CAD,
∴△ADF∽△ACD.
∴![]() .
.
∴AD2=AFAC.
∴AD2=6AF.
∴![]() .
.
∴当AD最短时,AF最短、CF最长.
当AD⊥BC时,AD最短,故AF最短、CF最长,此时![]() .
.
∴![]() .
.
∴![]() .
.


 优加精卷系列答案
优加精卷系列答案【题目】将正偶数按下表排成5列:
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
第一行 | 2 | 4 | 6 | 8 | |
第二行 | 16 | 14 | 12 | 10 | |
第三行 | 18 | 20 | 22 | 24 | |
第四行 | 32 | 30 | 28 | 26 | |
…… |
根据上面规律,2020应在( )
A.125行,3列B.125行,2列C.253行,2列D.253行,3列