题目内容
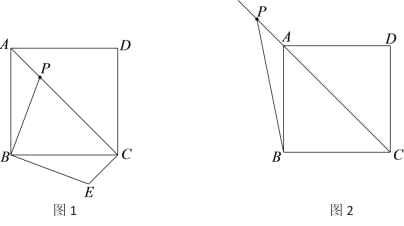
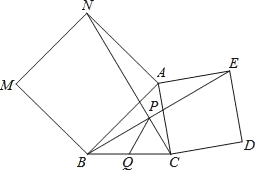
【题目】如图，已知矩形ABCD沿着直线BD折叠，使点C落在C/处，BC/交AD于E，AD=8，AB=4，DE的长=________________．
【答案】5
【解析】
首先根据矩形的性质可得出AD∥BC，即∠1=∠3，然后根据折叠知∠1=∠2，C′D=CD、BC′=BC，可得到∠2=∠3，进而得出BE=DE，设DE=x，则EC′=8-x，利用勾股定理求出x的值，即可求出DE的长．
∵四边形ABCD是矩形，
∴AD∥BC，即∠1=∠3，
由折叠知,∠1=∠2,C′D=CD=4、BC′=BC=8，
∴∠2=∠3，即DE=BE，
设DE=x,则EC′=8x，
在Rt△DEC′中,DC′2+EC′2=DE2
∴42+(8x)2=x2解得：x=5，
∴DE的长为5.
练习册系列答案
相关题目
【题目】某校组织了有奖征文活动，并设立了一、二、三等奖.根据设奖情况买了
件奖品，其中二等奖件数比一等奖件数的
倍少
件，各种奖品的单价如表所示:
一等奖 | 二等奖 | 三等奖 | |
单价/元 |
|
|
|
数量/件 |
|
如果计划一等奖买
件
(1)请把表填完整(填化简后的结果) .
(2)请用含有的代数式表示买件的总费用(写出解答过程并化简).
(3)若一等奖买件，则共花费多少元?
