题目内容
【题目】正方形![]() 中,点
中,点![]() 是直线
是直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
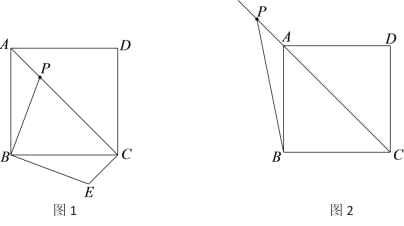
(1)如图1,若点![]() 在线段
在线段![]() 上,
上,
①直接写出![]() 的度数为 °;
的度数为 °;
②求证:![]() ;
;
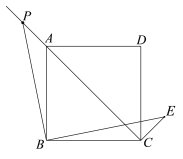
(2)如图2,若点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() ,
,
①依题意补全图2;
②直接写出线段![]() 的长度为 .
的长度为 .
【答案】(1)①![]() ;②证明见解析;(2)①补全图形见解析;②
;②证明见解析;(2)①补全图形见解析;②![]() .
.
【解析】
(1)①证明△BAP≌△BCE,得∠BAC=∠BCE=45°,从而可求出结论;
②连接![]() ,可得△PBE,△PCE均为直角三角形,利用勾股定理即可求解;
,可得△PBE,△PCE均为直角三角形,利用勾股定理即可求解;
(2)①根据提示补全图形即可;
②连接PE,可得△PBE,△PCE均为直角三角形,利用勾股定理求得PE=![]() ,PC=5,从而可求AC=4.
,PC=5,从而可求AC=4.
(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵∠PBE=90°,
∴∠ABP=∠CBE,
又BP=BE,
∴△BAP≌△BCE,
∴∠BAP=∠BCE
∵AC是正方形的对角线,
∴∠BAC=∠BCA=45°,
∴∠BCE=∠BCA=45°,
∴∠BCE+∠BCA=90°,即![]() 的度数为90°;
的度数为90°;
②证明:连接![]() ,如图.
,如图.

∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,![]() .
.
∵将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
![]() .
.
∴![]() ≌
≌![]() (
(![]() ).
).
∴![]() ,
,![]() .
.
∴![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
(2)①补全的图形如图所示.
②连接PE.易证△PBA≌△EBC,
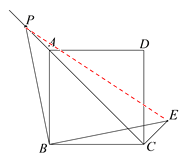
∴CE=PA=1,∠BAP=∠BCE,
∵四边形ABCD是正方形,
∴∠BAC=∠BCA=45°,
∴∠BAP=∠BCE=135°,
∴∠ECA=90°,即△PCE是直角三角形,
在Rt△PBE中,PE=![]() PB=
PB=![]() ,
,
在Rt△PCE中,PC=![]()
∴AC=PC-PA=5-1=4.

【题目】某林场要考察一种幼树在一定条件下的移植成活率,在移植过程中的统计结果如下表所示:
移植的幼树n/棵 | 500 | 1000 | 2000 | 4000 | 7000 | 10000 | 12000 | 15000 |
成活的幼树m/棵 | 423 | 868 | 1714 | 3456 | 6020 | 8580 | 10308 | 12915 |
成活的频率 | 0.846 | 0.868 | 0.857 | 0.864 | 0.860 | 0.858 | 0.859 | 0.861 |
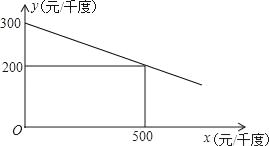
在此条件下,估计该种幼树移植成活的概率为_________________(精确到![]() );若该林场欲使成活的幼树达到4.3万棵,则估计需要移植该种幼树_________万棵.
);若该林场欲使成活的幼树达到4.3万棵,则估计需要移植该种幼树_________万棵.