题目内容
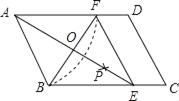
【题目】如图,在ABCD中,AB<BC,以点A为圆心,AB长为半径作圆弧交AD于点F,再分别以点B、F为圆心,大于BF的一半长为半径作圆弧,两弧交于一点P,连结AP并延长交BC于点E,连结EF.
(1)四边形ABEF是_____(填“矩形”、“菱形”、“正方形”或“无法确定”)(直接填写结果),并证明你的结论.
(2)AE、NF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为_____,∠ADC=_____°,(直接填写结果)
【答案】 菱形 ![]() 120°
120°
【解析】试题分析:(1)先证明![]() ≌
≌![]() ,推出
,推出![]() 由AD∥BC,推出
由AD∥BC,推出![]() 得到
得到![]() 由此即可证明.
由此即可证明.
(2)根据菱形的性质首先证明![]() 是含有30°的直角三角形,由此即可解决问题.
是含有30°的直角三角形,由此即可解决问题.
试题解析:(1)在△AEB和△AEF中,
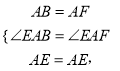
∴△AEB≌△AEF,
∴∠EAB=∠EAF,
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴BE=AB=AF.
∵AF∥BE,
∴四边形ABEF是平行四边形
∵AB=AF,
∴四边形ABEF是菱形.
故答案为:菱形.
(2)∵四边形ABEF是菱形,
∴AE⊥BF,BO=OF=5,∠ABO=∠EBO,
∵AB=10,
∴AB=2BO,
∵![]()
∴![]()
∴![]()
故答案为: ![]()

【题目】在学校组织的知识竞赛活动中,老师将八年级一班和二班全部学生的成绩整理并绘制成如下统计表:
得分(分) 人数(人) 班级 | 50 | 60 | 70 | 80 | 90 | 100 |
一班 | 2 | 5 | 10 | 13 | 14 | 6 |
二班 | 4 | 4 | 16 | 2 | 12 | 12 |
(1)现已知一班和二班的平均分相同,请求出其平均分.
(2)请分别求出这两班的中位数和众数,并进一步分析这两个班级在这次竞赛中成绩的情况.
【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产
辆自行车,平均每天生产![]() 辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产________辆;
根据记录可知前三天共生产________辆;
![]() 产量最多的一天比产量最少的一天多生产________辆;
产量最多的一天比产量最少的一天多生产________辆;
![]() 该厂实行计件工资制,每辆车
该厂实行计件工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?