题目内容
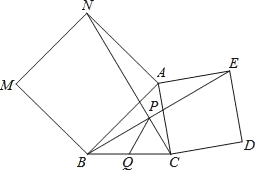
【题目】如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
探究:试判断BE和CN的位置关系和数量关系,并说明理由.
应用:Q是线段BC的中点,若BC=6,则PQ= .
【答案】见解析
【解析】试题分析:根据正方形性质得出AN=AB,AC=AE,∠NAB=∠CAE=90°,求出∠NAC=∠BAE,证出△ANC≌△ABE即可.
试题解析:解:CN=BE,BE⊥NC.理由如下:
∵四边形ANMB和四边形ACDE都是正方形,∴AN=AB,AC=AE,∠NAB=∠CAE=90°,∴∠NAB+∠BAC=∠CAE+∠BAC,∴∠NAC=∠BAE.
在△ANC和△ABE中,∵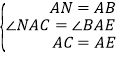 ,∴△ANC≌△ABE(SAS),∴CN=BE.
,∴△ANC≌△ABE(SAS),∴CN=BE.
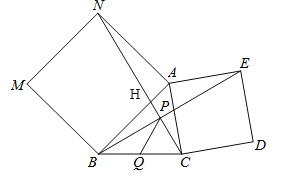
设CN交AB于H,交BE于P.∵△ANC≌△ABE,∴∠ABE=∠ANC.∵∠PHB=∠AHN,∴∠HPB=∠HAP=90°,∴BE⊥NC.∵四边形NABM是正方形,∴∠NAB=90°,∴∠ANC+∠AON=90°.∵∠BHP=∠AHN,∠ANC=∠ABE,∴∠ABP+∠BHP=90°,∴∠BPC=∠ABP+∠BHP=90°.∵Q为BC中点,BC=6,∴PQ=![]() BC=3.故答案为:3.
BC=3.故答案为:3.

 阅读快车系列答案
阅读快车系列答案【题目】某林场要考察一种幼树在一定条件下的移植成活率,在移植过程中的统计结果如下表所示:
移植的幼树n/棵 | 500 | 1000 | 2000 | 4000 | 7000 | 10000 | 12000 | 15000 |
成活的幼树m/棵 | 423 | 868 | 1714 | 3456 | 6020 | 8580 | 10308 | 12915 |
成活的频率 | 0.846 | 0.868 | 0.857 | 0.864 | 0.860 | 0.858 | 0.859 | 0.861 |
在此条件下,估计该种幼树移植成活的概率为_________________(精确到![]() );若该林场欲使成活的幼树达到4.3万棵,则估计需要移植该种幼树_________万棵.
);若该林场欲使成活的幼树达到4.3万棵,则估计需要移植该种幼树_________万棵.