题目内容
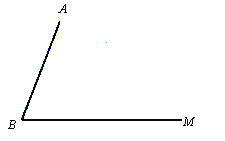
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
【答案】(1)画图见解析;(2)证明见解析.
【解析】试题分析:(1)①以点A为圆心,AB的长为半径画圆弧交射线BM与点C,连接AC;②以点B位圆心画一段圆弧分别交AB、BC于两点,然后分别以这两个点位圆心,画两段半径相等的圆弧并交于一点,连接此点与B点并延长交AC于点D;③以点C位圆心,CD的长为半径画圆弧交射线CM于点E,连接DE;(2)猜想BD=DE,要证明DE=BD,即要证明∠1=∠3,有题目已知条件不难得出∠1=![]() ∠4,∠3=
∠4,∠3=![]() ∠4,即可证明.
∠4,即可证明.
试题解析:
(1)如图所示:
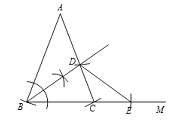
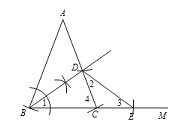
(2)BD= DE.
证明:∵BD平分∠ABC ,
∴∠1=![]() ∠ABC ,
∠ABC ,
∵ AB = AC ,
∴∠ABC=∠4,
∴∠1=![]() ∠4,
∠4,
∵CE=CD ,
∴∠2=∠3,
∵∠4=∠2+∠3,
∴∠3=![]() ∠4,
∠4,
∴∠1=∠3,
∴BD= DE .

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目