Question

【题目】已知：⊙O的两条弦，相交于点，且．

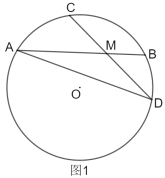
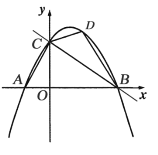
（1）如图1，连接，求证：．

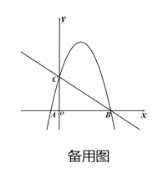
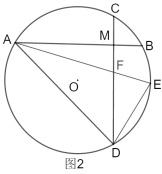
（2）如图2，在，在上取一点，使得，交于点，连接．

①判断与是否相等，并说明理由．

②若，，求的面积．

Answer 1

【答案】（1）见解析；（2）①相等，理由见解析；②．

【解析】

（1）根据弦，弧之间的关系得出，进而有，然后根据圆周角定理的推论即可得出，则结论可证；

（2）①连接AC，首先证明≌，则有，然后根据，和等量代换即可得出结论；

（3）设，则，然后利用DM=x+7和AM=DM建立一个关于x的方程，解方程即可求出x的值，从而AM可求，最后利用即可求解．

（1）∵，

，

，

∴，

∴；

（2）①相等，理由如下：

如图：连接AC，

∴，

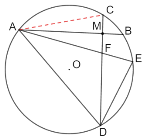
又∵，

∴，

又∵AM=AM，

∴≌（ASA）

∴，

又∵，

∴；

②由（1）知AM=DM，

设，

，

，

由①知：，

∴，

∵DE=7，

∴DF=7，

则：DM=x+7，

由AM=DM，得：17－x=x+7，解得：x=5,

∴AM=17－5=12，

∴．