题目内容
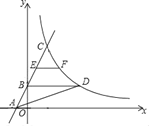
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

【答案】![]()
【解析】
根据矩形ABCD中,AB=3,BC=4,可得AC=5,由AE=![]() 可得点F是边BC上的任意位置时,点C始终在AC的下方,设点G到AC的距离为h,要使四边形AGCD的面积的最小,即h最小.所以点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.过点E作EH⊥AC,交圆E于点G,此时h最小.根据锐角三角函数先求得h的值,再分别求得三角形ACD和三角形ACG的面积即可得结论.
可得点F是边BC上的任意位置时,点C始终在AC的下方,设点G到AC的距离为h,要使四边形AGCD的面积的最小,即h最小.所以点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.过点E作EH⊥AC,交圆E于点G,此时h最小.根据锐角三角函数先求得h的值,再分别求得三角形ACD和三角形ACG的面积即可得结论.
解:如图,连接AC,

在矩形ABCD中,AB=3,BC=4,
∠B=∠D=90°,
∴AC=5,
∵AB=3,AE=![]() ,
,
∴点F是边BC上的任意位置时,点G始终在AC的下方,
设点G到AC的距离为h,
S四边形AGCD=S△ACD+S△ACG
=![]() 3×4+
3×4+![]() ×5h,
×5h,
=6+![]() h.
h.
要使四边形AGCD的面积的最小,即h最小.
∵点G在以点E为圆心,BE为半径的圆上,且在矩形ABCD的内部.
过点E作EH⊥AC,交圆E于点G,此时h最小.

在Rt△ABC中,sin∠BAC=![]() ,
,
在Rt△AEH中,AE=![]() ,
,
sin∠BAC=![]() ,
,
解得EH=![]() AE=
AE=![]() ,
,
EG=BE=AB﹣AE=3﹣![]() ,
,
∴h=EH﹣EG=![]() ﹣(3﹣
﹣(3﹣![]() )=
)=![]() ﹣3.
﹣3.
∴S四边形AGCD=6+![]() ×(
×(![]() ﹣3)
﹣3)
=![]() .
.
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲,乙,丙三名校排球队员每人10次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
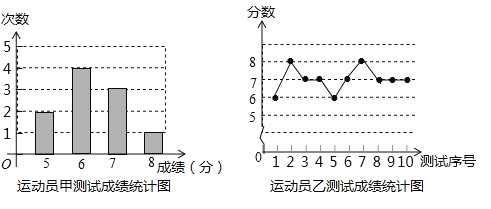
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
(1)若运动员丙测试成绩的平均数和众数都是7,则成绩统计表中![]() ,
,![]() ;
;
(2)若在三名队员中选择一位垫球成绩优秀且较为稳定的同学作为排球比赛的自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() ,
,![]() ,
,![]() )
)
(3)训练期间甲、乙、丙三人之间进行随机传球游戏,先由甲传出球,经过三次传球,球回到甲手中的概率是多少?