题目内容
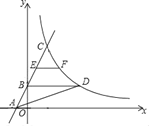
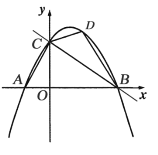
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点B、C,经过点B、C的抛物线
轴相交于点B、C,经过点B、C的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求出抛物线表达式,并求出点A坐标;
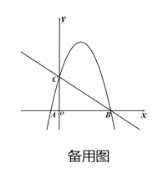
(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于![]() 轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2+
x2+![]() x+4,A(-1,0);(2)18;(3)P(5,4)或P(
x+4,A(-1,0);(2)18;(3)P(5,4)或P(![]() ,
,![]() )时,点A、P、Q为顶点的三角形与△BOC相似.
)时,点A、P、Q为顶点的三角形与△BOC相似.
【解析】
(1)求出B(6,0),C(0,4)并代入y=-![]() x2+bx+c,即可求出解析式;
x2+bx+c,即可求出解析式;
(2)求出D(3,8),过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;则E(0,8),F(6,8),所以S△BCD=S梯形ECBF-S△CDE-S△BFD=![]() (EC+BF)×OB-
(EC+BF)×OB-![]() ×EC×ED-
×EC×ED-![]() ×DF×BF,再由所求点确定各边长即可求面积;
×DF×BF,再由所求点确定各边长即可求面积;
(3)点A、P、Q为顶点的三角形与△BOC相似有两种情况:①△PAQ∽△CBO时,由![]() ,则
,则![]() ,求出m;②△PAQ∽△BCO时,
,求出m;②△PAQ∽△BCO时,![]() ,则有
,则有![]() ,求出m.
,求出m.
(1)由已知可求B(6,0),C(0,4),
将点B(6,0),C(0,4)代入y=-![]() x2+bx+c,
x2+bx+c,
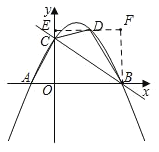
则有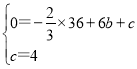 ,
,
解得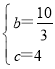 ,
,
∴y=-![]() x2+
x2+![]() x+4,
x+4,
令y=0,则-![]() x2+
x2+![]() x+4=0,
x+4=0,
解得x=-1或x=6,
∴A(-1,0);
(2)∵点D在抛物线上,且横坐标为3,
∴D(3,8),
过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;
∴E(0,8),F(6,8),
∴S△BCD=S梯形ECBF-S△CDE-S△BFD=![]() (EC+BF)×OB-
(EC+BF)×OB-![]() ×EC×ED-
×EC×ED-![]() ×DF×BF
×DF×BF
=![]() ×(4+8)×6-
×(4+8)×6-![]() ×4×3-
×4×3-![]() ×3×8
×3×8
=36-6-12
=18;
(3)设P(m,-![]() m2+
m2+![]() m+4),
m+4),
∵PQ垂直于x轴,
∴Q(m,0),且∠PQO=90°,
∵∠COB=90°,
∴点A、P、Q为顶点的三角形与△BOC相似有两种情况:
①△PAQ∽△CBO时,![]() ,
,
∴![]() ,
,
解得m=5或m=-1,
∵点P是直线BC上方的抛物线上,
∴0≤m≤6,
∴m=5,
∴P(5,4);
②△PAQ∽△BCO时,![]() ,
,
∴![]() ,
,
解得m=-1或m=![]() ,
,
∵点P是直线BC上方的抛物线上,
∴0≤m≤6,
∴m=![]() ,
,
∴P(![]() ,
,![]() );
);
综上所述:P(5,4)或P(![]() ,
,![]() )时,点A、P、Q为顶点的三角形与△BOC相似.
)时,点A、P、Q为顶点的三角形与△BOC相似.

【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
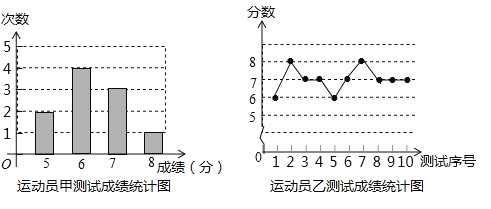
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲,乙,丙三名校排球队员每人10次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
(1)若运动员丙测试成绩的平均数和众数都是7,则成绩统计表中![]() ,
,![]() ;
;
(2)若在三名队员中选择一位垫球成绩优秀且较为稳定的同学作为排球比赛的自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() ,
,![]() ,
,![]() )
)
(3)训练期间甲、乙、丙三人之间进行随机传球游戏,先由甲传出球,经过三次传球,球回到甲手中的概率是多少?