题目内容
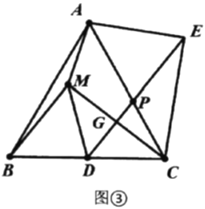
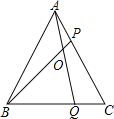
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
【答案】4,![]() .
.
【解析】
先通过条件证明△ABP≌△ACQ,得到∠ABP=∠CAQ,可证明△APO∽△BPA,得出![]() ,则AP2=OPBP,可求出AP,设OA=x,则AB=2x,在Rt△ABE中,由AE2+BE2=AB2,得出x的值即可得解.
,则AP2=OPBP,可求出AP,设OA=x,则AB=2x,在Rt△ABE中,由AE2+BE2=AB2,得出x的值即可得解.
解:解:∵△ABC是等边三角形
∴∠BAP=∠ACQ=∠ABQ=60°,AB=AC=BC,
∵在△ABP和△ACQ中
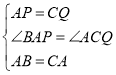 ,
,
∴△ABP≌△ACQ (SAS),
∴∠ABP=∠CAQ,
∵∠APO=∠BPA,
∴△APO∽△BPA,
∴![]() ,
,
∴AP2=OPBP,
∵BO=6,PO=2,
∴BP=8,
∴AP2=2×8=16,
∴AP=4,
∵∠BAC=60°,
∴∠BAQ+∠CAQ=60°,
∴∠BAQ+∠ABP=60°,
∵∠BOQ=∠BAQ+ABP,
∴∠BOQ=60°,
过点B作BE⊥OQ于点E,
∴∠OBE=30°,
∵OB=6,
∴OE=3,BE=3![]() ,
,
∵![]() ,
,
设OA=x,则AB=2x,
在Rt△ABE中,AE2+BE2=AB2,
∴(x+3)2+(3![]() )2=(2x)2,
)2=(2x)2,
解得:x=![]() 或x=1-
或x=1-![]() (舍去),
(舍去),
∴AO=1+![]() .
.
故答案为:4,![]() .
.

练习册系列答案
相关题目