Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ∂®“Ś£ļĶĪĶ„P‘ŕ…šŌŖOA…Ō Ī£¨į—![]() ĶńĶń÷ĶĹ–◊ŲĶ„P‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķ£ĽĶĪĶ„P≤Ľ‘ŕ…šŌŖOA…Ō Ī£¨į—…šŌŖOA…Ō”ŽĶ„P◊ÓĹŁĶ„Ķń…š”į÷Ķ£¨Ĺ–◊ŲĶ„P‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķ£ģ
ĶńĶń÷ĶĹ–◊ŲĶ„P‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķ£ĽĶĪĶ„P≤Ľ‘ŕ…šŌŖOA…Ō Ī£¨į—…šŌŖOA…Ō”ŽĶ„P◊ÓĹŁĶ„Ķń…š”į÷Ķ£¨Ĺ–◊ŲĶ„P‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķ£ģ
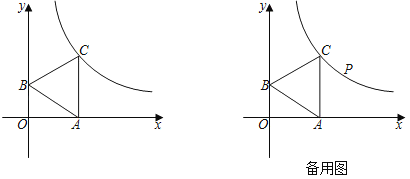
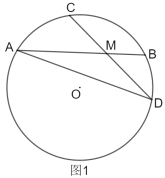
ņż»Á£ļ»ÁÕľ1£¨°ųOAB»żłŲ∂•Ķ„ĺý‘ŕłŮĶ„…Ō£¨BP «OAĪŖ…ŌĶńłŖ£¨‘ÚĶ„PļÕĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķĺýő™![]() £Ĺ
£Ĺ![]() £ģ
£ģ

£®1£©‘ŕ°ųOAB÷–£¨
ĘŔĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķ–°”ŕ1 Ī£¨‘Ú°ųOAB «»ŮĹ«»żĹ«–ő£Ľ
ĘŕĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷ĶĶ»”ŕ1 Ī£¨‘Ú°ųOAB «÷ĪĹ«»żĹ«–ő£Ľ
ĘŘĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķīů”ŕ1 Ī£¨‘Ú°ųOAB «∂ŘĹ«»żĹ«–ő£ģ
∆š÷–’ś√ŁŐ‚”–°° °°£ģ
A£ģĘŔĘŕB£ģĘŔĘŘC£ģĘŕĘŘD£ģĘŔĘŕĘŘ
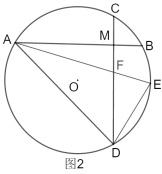
£®2£©“—÷™£ļĶ„C «…šŌŖOA…Ō“ĽĶ„£¨CA£ĹOA£Ĺ1£¨“‘©Ėő™‘≤–ń£¨OAő™įŽĺ∂Ľ≠‘≤£¨Ķ„B «°—O…Ō»ő“‚Ķ„£ģ
ĘŔ»ÁÕľ2£¨»ŰĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķő™![]() £ģ«ů÷§£ļ÷ĪŌŖBC «°—OĶń«–ŌŖ£Ľ
£ģ«ů÷§£ļ÷ĪŌŖBC «°—OĶń«–ŌŖ£Ľ
Ęŕ»ÁÕľ3£¨“—÷™Dő™ŌŖ∂őBCĶń÷–Ķ„£¨…ŤĶ„D‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķő™x£¨Ķ„D‘ŕ…šŌŖOB…ŌĶń…š”į÷Ķő™y£¨÷ĪĹ”–ī≥Ųy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺő™°° °°£ģ
°ĺīūįł°Ņ£®1£©B£Ľ£®2£©ĘŔ÷§√ųľŻĹ‚őŲ£ĽĘŕy£Ĺ0£®![]() °‹x°‹
°‹x°‹![]() £©ĽÚy£Ĺ2x©Ā
£©ĽÚy£Ĺ2x©Ā![]() £®
£®![]() £ľx°‹
£ľx°‹![]() £©£ģ
£©£ģ
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›…š”į÷ĶĶń∂®“Ś“Ľ“ĽŇ–∂ŌľīŅ…£ģ
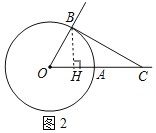
£®2£©ĘŔłýĺ›ŃĹĪŖ≥…Ī»ņżľ–Ĺ«ŌŗĶ»ĶńŃĹłŲ»żĹ«–őŌŗň∆£¨Ņ…Ķ√°ųBOH°◊°ųCOB£¨”…Ōŗň∆»żĹ«–őĶń–‘÷ Ņ…Ķ√°ŌBHO£Ĺ°ŌCBO£Ĺ90°„£¨łý囫–ŌŖĶńŇ–∂®∂®ņŪŅ…Ķ√īūįł£Ľ
ĘŕÕľ–ő «…ŌŌ¬∂‘≥∆Ķń£¨÷ĽŅľ¬«B‘ŕ÷ĪŌŖOC…ŌľįOC…Ō∑Ĺ≤Ņ∑÷Ķń«ť–ő£ģ∑÷ŃĹ÷÷«ťŅŲŅľ¬«£ļĶĪ°ŌDOB£ľ90°„ Ī£ĽĶĪ°ŌBOD£Ĺ90°„ Ī£ģ
Ĺ‚£ļ£®1£©ĘŔīŪőů£ģĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķ–°”ŕ1 Ī£¨°ŌOBAŅ…“‘ «∂ŘĹ«£¨Ļ °ųOAB≤Ľ“Ľ∂® «»ŮĹ«»żĹ«–ő£Ľ
Ęŕ’ż»∑£ģĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷ĶĶ»”ŕ1 Ī£¨AB°ÕOA£¨°ŌOAB£Ĺ90°„£¨°ųOAB «÷ĪĹ«»żĹ«–ő£Ľ
ĘŘ’ż»∑£ģĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķīů”ŕ1 Ī£¨°ŌOAB «∂ŘĹ«£¨Ļ °ųOAB «∂ŘĹ«»żĹ«–ő£Ľ
Ļ īūįłő™£ļB£ģ
£®2£©ĘŔ»ÁÕľ2£¨◊ųBH°ÕOC”ŕĶ„H£¨
°ŖĶ„B‘ŕ…šŌŖOA…ŌĶń…š”į÷Ķő™![]() £¨
£¨
°ŗ![]() £Ĺ
£Ĺ![]() £¨
£¨![]() £Ĺ
£Ĺ![]() £¨CA£ĹOA£ĹOB£Ĺ1£¨
£¨CA£ĹOA£ĹOB£Ĺ1£¨
°ŗ![]() £Ĺ
£Ĺ![]() £¨
£¨
”÷°Ŗ°ŌBOH£Ĺ°ŌCOB£¨
°ŗ°ųBOH°◊°ųCOB£¨
°ŗ°ŌBHO£Ĺ°ŌCBO£Ĺ90°„£¨
°ŗBC°ÕOB£¨
°ŗ÷ĪŌŖBC «°—OĶń«–ŌŖ£Ľ
ĘŕÕľ–ő «…ŌŌ¬∂‘≥∆Ķń£¨÷ĽŅľ¬«B‘ŕ÷ĪŌŖOC…ŌľįOC…Ō∑Ĺ≤Ņ∑÷Ķń«ť–ő£ģĻżĶ„D◊ųDM°ÕOC£¨◊ųDN°ÕOB£¨
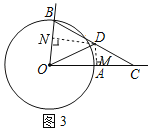
ĶĪ°ŌDOB£ľ90°„ Ī£¨…ŤDM£Ĺh£¨
°ŖDő™ŌŖ∂őBCĶń÷–Ķ„£¨
°ŗS°ųOBD£ĹS°ųODC£¨
°ŗ![]() OB°ŃDN£Ĺ
OB°ŃDN£Ĺ![]() OC°ŃDM£¨
OC°ŃDM£¨
°ŗDN£Ĺ2h£¨
°Ŗ‘ŕRt°ųDONļÕRt°ųDOM÷–£¨
OD2£ĹDN2+ON2£ĹDM2+OM2£¨
°ŗ4h2+y2£Ĺh2+x2£¨
°ŗ3h2£Ĺx2©Āy2ĘŔ£¨
°ŖBD2£ĹCD2£¨
°ŗ4h2+£®1©Āy£©2£Ĺh2+£®2©Āx£©2Ęŕ£¨
ĘŔĘŕŌŻ»•hĶ√£ļy£Ĺ2x©Ā![]() £ģ
£ģ
»ÁÕľ£¨ĶĪ°ŌBOD£Ĺ90°„ Ī£¨ĻżĶ„D◊ųDM°ÕOC”ŕĶ„M£¨
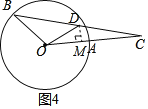
°ŖDő™ŌŖ∂őBCĶń÷–Ķ„£¨
°ŗS°ųOBD£ĹS°ųODC£¨
°ŗ![]() OB°ŃDO£Ĺ
OB°ŃDO£Ĺ![]() OC°ŃDM£¨
OC°ŃDM£¨
°ŖCA£ĹOA£ĹOB£Ĺ1£¨
°ŗOD£Ĺ2DM£¨
°ŗsin°ŌDOM£Ĺ![]() £¨
£¨
°ŗ°ŌDOM£Ĺ30°„£¨
…ŤDM£Ĺh£¨‘ÚOD£Ĺ2h£¨OM£Ĺ![]() h£¨
h£¨
°ŗh2+![]() £Ĺ1+4h2£¨
£Ĺ1+4h2£¨
°ŗh£Ĺ![]() £¨
£¨
°ŗOM£Ĺ![]() £¨
£¨
ĶĪĶ„B‘ŕOC…Ō Ī£¨OD£Ĺ![]() £¨
£¨
◊Ř…Ōňý Ų£¨ĶĪ![]() °‹x°‹
°‹x°‹![]() Ī£¨y£Ĺ0£ĽĶĪ
Ī£¨y£Ĺ0£ĽĶĪ![]() £ľx°‹
£ľx°‹![]() Ī£¨y£Ĺ2x©Ā
Ī£¨y£Ĺ2x©Ā![]() £ģ
£ģ
Ļ īūįłő™£ļy£Ĺ0£®![]() °‹x°‹
°‹x°‹![]() £©ĽÚy£Ĺ2x©Ā
£©ĽÚy£Ĺ2x©Ā![]() £®
£®![]() £ľx°‹
£ľx°‹![]() £©£ģ
£©£ģ

 ‘ń∂ŃŅž≥ĶŌĶŃ–īūįł
‘ń∂ŃŅž≥ĶŌĶŃ–īūįł