题目内容
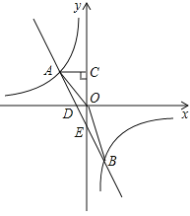
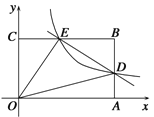
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为（6，4）．双曲线
经过AB的中点D，且与BC交于点E，连接DE．
（1）求k的值和直线DE的解析式；
（2）若点P是y轴上一点，且△OPE的面积与四边形ODBE的面积相等，求点P的坐标．
【答案】（1）
；（2）
或
【解析】
（1）根据AB的中点D（6，2）求得双曲线解析式，继而结合矩形的性质知点E（3，4），待定系数法求得直线DE的解析式；
（2）先利用割补法求得四边形的面积，再依据△OPE的面积与四边形ODBE的面积相等求得点P的纵坐标即可得出答案．
解：（1）∵点B的坐标为（6，4），
∴AB的中点D的坐标为（6，2），
将点D（6，2）的坐标代入
，得k=6×2=12．
∵BC∥x轴，∴点E的纵坐标与点B的纵坐标相等，
∴点E的纵坐标为4．
∵点E在双曲线上，
∴
，
∴点E在坐标为（3，4）
设直线DE的解析式为
，
将点D（6，2）、E（3，4）的坐标代入，
得
，解得：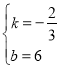
．
∴直线DE的解析式为：
（2）∵S四边形ODBE=S矩形OABC-S△OAD-S△OCE
=6×4-
×6×2-×4×3=12，
∴
，即
，
∴OP=8
∴点P的坐标为（0，8）或（0，-8）
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
