Question

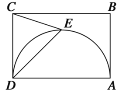
【题目】如图，在矩形ABCD中，AD＝6，AB＝4，以AD为直径在矩形内作半圆，点E为半圆上的一动点（不与A、D重合），连接DE、CE，当△DEC为等腰三角形时，DE的长为_____．

Answer 1

【答案】4或

【解析】

分四种情形分别求解即可解决问题．

①当DE=DC时，△CDE是等腰三角形，此时DE=DC=AB=4．

②当CD=CE时，△CDE是等腰三角形．

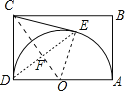
此时CD、CE是⊙O的切线，连接OC交DE于F．

∵CD=CE，OD=OE，

∴OC垂直平分线段DE，

∴DF=EF=，

∴．

③当EC=ED时，△ECD是等腰三角形．

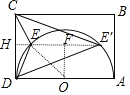
作EH⊥CD于H，交⊙O于E′，作OF⊥EE′．

在Rt△EFO中，，

∴，

∴，

，

综上所述，DE的长为4或或或．

故答案为4或或或．