Question

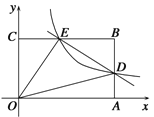
【题目】甲、乙两地之间有一条笔直的公路，小明从甲地出发步行前往乙地，同时小亮从乙地出发骑自行车前往甲地，小亮到达甲地没有停留，按原路原速返回，追上小明后两人一起步行到乙地．如图，线段OA表示小明与甲地的距离y1（米）与行走的时间x（分钟）之间的函数关系：折线BCDA表示小亮与甲地的距离y2（米）与行走的时间x（分钟）之间的函数关系．请根据图象解答下列问题：

（1）小明步行的速度是　 　米/分钟，小亮骑自行车的速度是　 　米/分钟；

（2）线段OA与BC相交于点E，求点E坐标；

（3）请直接写出小亮从乙地出发到追上小明的过程中，与小明相距100米时x的值．

Answer 1

【答案】（1）50，150；（2）（7.5，375）；（3）7，8或14

【解析】

（1）根据题意和图象中的数据，可以得到小明步行的速度和小亮骑车的速度；

（2）根据（1）中的结果，可以计算出点E坐标；

（3）根据题意，可知有三种情况，两人相距100米，然后分别计算出x的值即可．

（1）由图可知，

小明步行的速度为1500÷30＝50（米/分钟），

小亮骑车的速度为1500÷10＝150（米/分钟），

故答案为：50，150；

（2）点E的横坐标为：1500÷（50+150）＝7.5，纵坐标为：50×7.5＝375，

即点E的坐标为（7.5，375）；

（3）小亮从乙地出发到追上小明的过程中，与小明相距100米时x的值是7，8或14．

理由：两人相遇前，（50+150）x+100＝1500，得x＝7，

两人相遇后，（50+150）x﹣100＝1500，得x＝8，

小亮从甲地到追上小明时，50x﹣100＝150（x﹣10），得x＝14，

即小亮从乙地出发到追上小明的过程中，与小明相距100米时x的值是7，8或14．