题目内容
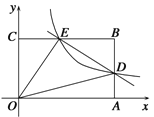
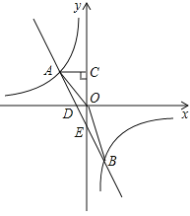
【题目】如图,在平面直角坐标系中,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于
的图象交于![]() 两点,点
两点,点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,
, ![]() 的面积是3,一次函数
的面积是3,一次函数![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)求![]() 的面积.
的面积.
【答案】(1)y=![]() ,y=-2x-1;(2)
,y=-2x-1;(2)![]()
【解析】
(1)根据![]() AOC的面积是3得到k=﹣6,于是得到反比例函数的解析式为y=
AOC的面积是3得到k=﹣6,于是得到反比例函数的解析式为y=![]() ,把B(m,﹣4)代入y=
,把B(m,﹣4)代入y=![]() 得到B(
得到B(![]() ,﹣4),设A(﹣m,n),根据已知条件得到A(﹣2,3),把A(﹣2,3),B(
,﹣4),设A(﹣m,n),根据已知条件得到A(﹣2,3),把A(﹣2,3),B(![]() ,﹣4)代入y=ax+b得到一次函数的解析式为:y=﹣2x﹣1;
,﹣4)代入y=ax+b得到一次函数的解析式为:y=﹣2x﹣1;
(2)根据三角形的面积公式即可得到结论.
解:(1)∵![]() AOC的面积是3,
AOC的面积是3,
∴k=-6,
∴反比例函数的表达式为y=![]() .
.
∵B(m,-4)在反比例函数y=![]() 的图象上,
的图象上,
∴-4m=-6,
∴m=![]() ,
,
∴B(![]() ,-4).
,-4).
设A(-m,n)(m>0,n>0),
∵tan∠AOC=![]() ,
,![]() AOC的面积是3,
AOC的面积是3,
∴![]() =
=![]() ,mn=6,
,mn=6,
∴m=2,n=3,
∴A(-2,3).
把A(-2,3),B(![]() ,-4)代入y=ax+b,
,-4)代入y=ax+b,
得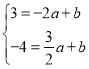
解得![]()
∴一次函数的表达式为y=-2x-1.
(2)令x=0,则y=-1,
∴E(0,-1),
∴OE=1,
∴S△AOB=S△AOE+S△BOE
=![]() ×1×2+
×1×2+![]() ×1×
×1×![]()
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了调查某小区居民的用水情况,随机抽查了若干个家庭的![]() 月份用水量,结果如下表:
月份用水量,结果如下表:
月用水量(立方米) |
|
|
|
|
户数 |
|
|
|
|
根据上表解决下列问题:
(1)这组数据的众数是 ,中位数是 ;
(2)求这若干个家庭的![]() 月份平均用水量;
月份平均用水量;
(3)请根据(2)的结论估计该小区![]() 个家庭
个家庭![]() 月份总用水量.
月份总用水量.
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?