题目内容
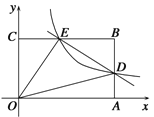
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.
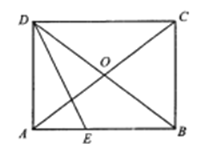
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)AE=3.
【解析】
(1)由平行四边形的性质及![]() 可得该四边形的对角线相等,即可证明四边形
可得该四边形的对角线相等,即可证明四边形![]() 是矩形;
是矩形;
(2)过点E作EG⊥BD于点G,由角平分线的性质得EG=EA,证出Rt△ADE≌Rt△GDE,根据矩形的性质计算各边的长度,在Rt△BEG中,由勾股定理得![]() ,代入数据计算即可求解.
,代入数据计算即可求解.
(1)证明:∵四边形ABCD是平行四边形,
∴AC=2AO,BD=2BO.
∵AO=BO,
∴AC=BD.
∴平行四边形ABCD为矩形.
(2)解:过点E作EG⊥BD于点G,
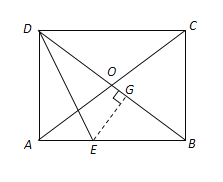
∵矩形ABCD,OC=5,
∴BD=8.
在Rt△ABD中,
∵AB=8,BD=10
∴![]()
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴EA⊥AD于点A,
∵DE为∠ADB的平分线,
又EG⊥BD于点G,
∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,
![]()
∴Rt△ADE≌Rt△GDE(HL)
∴AD=GD=6
在Rt△BEG中,
∵![]()
∴![]()
![]()
∴AE=3.

【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
【题目】为了传承中华优秀传统文化,某校组织了一次全校![]() 名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于
名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于![]() 分,为了更好的了解本次大赛的成绩分布情况,随机抽取了
分,为了更好的了解本次大赛的成绩分布情况,随机抽取了![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
取整数,总分![]() 分)作为样本进行整理,得到下列不完整的统计图表:
分)作为样本进行整理,得到下列不完整的统计图表:
成绩在这![]() 组的数据是:
组的数据是:
![]()
![]()
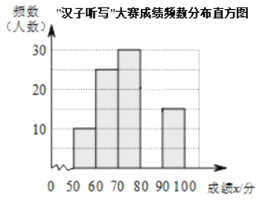
“汉字听写”大赛成绩段频数频率统计表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)表中![]() ,
,![]() ;
;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生获得优胜奖,估计该校参加这次比赛的
分)的学生获得优胜奖,估计该校参加这次比赛的![]() 名学生中获得优胜奖的人数.
名学生中获得优胜奖的人数.