题目内容
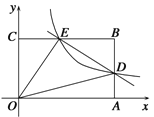
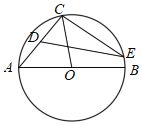
【题目】如图，一次函数
图象与反比例函数
的图象交于点
、
，与
轴交于点
．
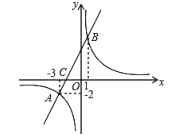
（1）求一次函数与反比例函数的解析式．
（2）求点坐标．
（3）平面上的点
与点
、、构成平行四边形，请直接写出满足条件的点坐标______．
【答案】（1）
，
；（2）
；（3）
或
或
【解析】
(1)先由图形得出的信息代入求出m,再求出B点,利用待定系数法将A、B代入求出即可.
(2)一次函数令y=0求出x即可得出C坐标.
(3)根据题意分别找到点所在的直线,再根据线段长度判断即可.
解：（1）把
代入
得：
，
把
横坐标
代入得：
，即
，
把
，
代入
得：
，
解得：
，
∴一次函数解析式为；反比例函数的解析式.
（2）对于，
令
，得到
，
则
的坐标为；
（3）如下图所示，分三种情况考虑：
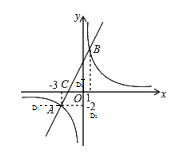
O、C、A三点确定,D点满足题意得点必定在y轴上或过点A平行x轴的平行线上,
在y轴上可得(1,2)、(﹣1,﹣2)满足
在过A点平行x轴的平行线上可得(﹣5,﹣2),(﹣1,﹣2)满足
综上所述：
；
；
．
故答案为：或或.
练习册系列答案
相关题目
【题目】为了传承中华优秀传统文化，某校组织了一次全校
名学生参加的“汉字听写”大赛，并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于
分，为了更好的了解本次大赛的成绩分布情况，随机抽取了
名学生的成绩(成绩
取整数，总分分)作为样本进行整理，得到下列不完整的统计图表：
成绩在这
组的数据是：
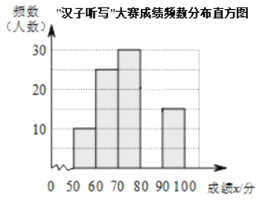
“汉字听写”大赛成绩段频数频率统计表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上信息，解答下列问题:
（1）表中
，
；
（2）请补全频数分布直方图；
（3）这次比赛成绩的中位数是 ；
（4）若这次比赛成绩在
分以上(含分)的学生获得优胜奖，估计该校参加这次比赛的名学生中获得优胜奖的人数．
