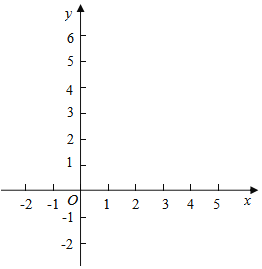题目内容
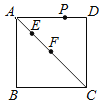
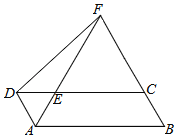
【题目】如图,在ABCD中,∠ABC=60°,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接DF.
(1)求证:△ABF是等边三角形;
(2)若∠CDF=45°,CF=2,求AB的长度.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据在ABCD中,∠ABC=60°,可以得到∠DAB的度数,然后根据AF平分∠DAB,可以得到∠FAB的度数,然后等边三角形的判定方法即可得到△ABF是等边三角形;
(2)作FG⊥DC于点G,然后根据直角三角形中30°角所对的直角边等于斜边的一半,可以得到CG、FG的长,然后即可得到DG的长,从而可以得到DC的长,然后即可得到AB的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DAB+∠ABC=180°,
∵∠ABC=60°,
∴∠DAB=120°,
∵AF平分∠DAB,
∴∠FAB=60°,
∴∠FAB=∠ABF=60°,
∴∠FAB=∠ABF=∠AFB=60°,
∴△ABF是等边三角形;
(2)作FG⊥DC于点G,
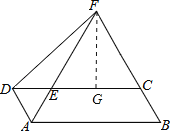
∵四边形ABCD是平行四边形,∠ABC=60°,
∴DC∥AB,DC=AB,
∴∠FCG=∠ABC=60°,
∴∠GFC=30°,
∵CF=2,∠FGC=90°,
∴CG=1,FG=![]() ,
,
∵∠FDG=45°,∠FGD=90°,
∴∠FDG=∠DFG=45°,
∴DG=FG=![]() ,
,
∴DC=DG+CG=![]() ,
,
∴AB=![]() ,
,
即AB的长度是![]() .
.

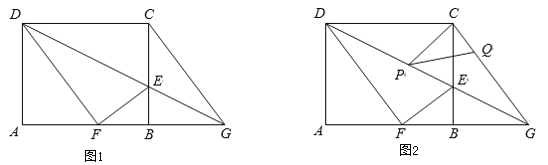
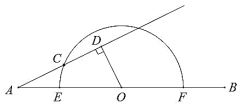
【题目】如图,点![]() 是线段
是线段![]() 的中点,
的中点,![]() 是以
是以![]() 为圆心,
为圆心,![]() 长为直径的半圆弧,点
长为直径的半圆弧,点![]() 是
是![]() 上一动点,过点
上一动点,过点![]() 作射线
作射线![]() 的垂线,垂足为
的垂线,垂足为![]() .已知
.已知![]() ,
,![]() ,设
,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
小丽根据学习函数的经验,分别对函数![]() 和
和![]() 随自变量
随自变量![]() 变化而变化的规律进行了探究.下面是小丽的探究过程,请将它补充完整:
变化而变化的规律进行了探究.下面是小丽的探究过程,请将它补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到
的值进行取点、画图、测量,分别得到![]() 和
和![]() 与
与![]() 的几组对应值:
的几组对应值:
| 2 | 3 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 |
| 0 | 2.76 |
| 2.96 | 2.86 | 2.70 | 2.49 | 1.85 | 0 |
| 3.00 | 1.18 | 0 | 0.47 | 0.90 | 1.30 | 1.37 | 2.36 | 3.00 |
经测量,![]() 的值是______;(保留一位小数)
的值是______;(保留一位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() 和
和![]() ,并画出函数
,并画出函数![]() 、
、![]() 的图象;
的图象;
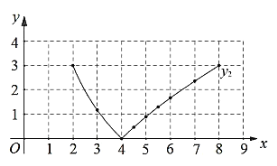
(3)结合函数图象,解决问题:连接![]() ,当
,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长度约为______
的长度约为______![]() .(结果保留一位小数)
.(结果保留一位小数)
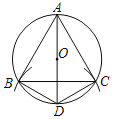
【题目】如图,C是![]() 上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.小石根据学习函数的经验,对线段PC,PA,AQ的长度之间的关系进行了探究.(当点P与点A重合时,令AQ=0cm)
上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.小石根据学习函数的经验,对线段PC,PA,AQ的长度之间的关系进行了探究.(当点P与点A重合时,令AQ=0cm)
下面是小石的探究过程,请补充完整:
(1)对于点P在弦AB上的不同位置,画图、测量,得到了线段PC,PA,AQ的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
在PC,PA,AQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ=PC时,PA的长度约为 cm.(结果保留一位小数)