题目内容
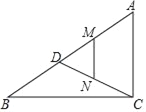
【题目】已知:如图, AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD , 作BE∥OD交⊙O于点E, 联结DE并延长交BN于点C.
(1)求证:DC是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长.

【答案】(1)证明见解析;(2)4.
【解析】
试题(1)连接OE,由OE=OB,利用等边对等角得到一对角相等,再由OD与BE平行,得到一对同位角及一对内错角相等,等量代换得到∠AOD=∠OBE=∠OEB=∠EOD,再由OA=OE,OD=OD,利用SAS得到三角形AOD与三角形EOD全等,由全等三角形对应角相等得到∠OAD=∠OED,根据AM为圆O的切线,利用切线的性质得到∠OAD=∠OED=90°,即可得证.
(2)过点D作BC的垂线,垂足为H,由BN与圆O切线于点B,得到∠ABC=90°=∠BAD=∠BHD,利用三个角为直角的四边形为矩形得到ADHB为矩形,利用矩形的对边相等得到BH=AD=1,AB=DH,由BC-BH求出HC的长,AD、CB、CD分别切⊙O于点A、B、E,利用切线长定理得到AD=DE=1,EC=BC=4,在直角三角形DHC中,利用勾股定理求出DH的长,即为AB的长.
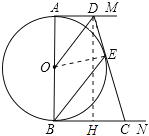
试题解析:(1)如图,连接OE,
在⊙O中,OA=OE=OB,∴∠OBE=∠OEB.
∵OD∥BE,∴∠AOD=∠OBE=∠OEB=∠EOD.
在△AOD和△EOD中,OA=OE,∠AOD=∠EOD,OD=OD,
∴△AOD≌△EOD(SAS).∴∠OAD=∠OED.
∵AM是⊙O的切线,切点为A,∴BA⊥AM.
∴∠OAD=∠OED=90°.∴OE⊥DE.
∵OE是⊙O的半径,∴DE是⊙O的切线.
(2)如图,过点D作BC的垂线,垂足为H,
∵BN切⊙O于点B,∴∠ABC=90°=∠BAD=∠BHD.∴四边形ABHD是矩形.
∴AD=BH=1,AB=DH,∴CH=BC-BH=4-1=3.
∵AD、CB、CD分别切⊙O于点A、B、E,∴AD=ED=1,BC=CE=4.
∴DC=DE+CE=1+4=5,
在Rt△DHC中,![]() ,
,
∴![]() .
.

 全优点练单元计划系列答案
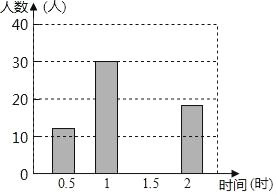
全优点练单元计划系列答案【题目】某校倡议八年级学生利用双休日在各自社区参加义务劳动.为了了解同学们参加义务劳动的时间,学校随机调查了部分同学参加义务劳动的时间,用得到的数据绘制成如下不完整的统计图表:
劳动时间(时) | 频数(人) | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.4 |
2 | 18 | y |
合计 | m | 1 |
(1)统计表中的m=_____,x=______,y=_______;
(2)请将频数分布直方图补充完整;
(3)求被调查同学的平均劳动时间.